Artikel
Ein Ding drehen
Flimmerfreies, räumliches Drehen
von Drahtmodellen mit Turbo Pascal
Haben Sie schon mal ein Ding gedreht – auf dem Bildschirm natürlich – und sich gefragt, wie das entsprechende 3D-Programm funktioniert? Die Antwort gibt dieser Artikel in Form eines Turbo-Pascal-Programms, das gestattet, selbstentworfene Drahtmodelle mit den Cursortasten auf dem Monitor zu bewegen.
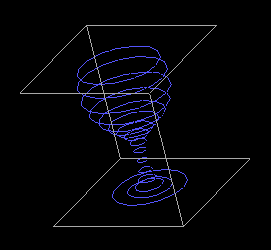
Computergrafik gehört zu den faszinierendsten Gebieten der PC-Anwendungen. Dies gilt insbesondere dann, wenn es sich um dreidimensionale Darstellungen handelt, die zudem noch bewegt sind. Einige Grundlagen für grafische Experimente in der dritten Dimension vermitteln wir Ihnen hier. Dabei werden die mathematischen Hilfsmittel nur kurz angerissen, detailliertere Darstellungen lassen sich in Schulbüchern der gymnasialen Oberstufe, in Nachschlagewerken der Mathematik oder in Spezialliteratur finden [1], [3].
Ein Körper ist relativ einfach in Form eines Drahtmodelles zu beschreiben. Hierfür ist es praktisch, mit einer orthonormalen Basis zu arbeiten, das heißt, daß alle Achsen des Koordinatensystems jeweils senkrecht aufeinander stehen und die gleichen Maßeinheiten benutzen. Für eine begrenzte Anzahl von Punkten auf der Oberfläche des Objektes gibt man deren Koordinaten an. Durch Verbindung der einzelnen Punkte ensteht das Drahtmodell.
Will man ein solches Modell verschieben, drehen
oder in der Größe ändern, ist es sinnvoll, die Punkte
als Endpunkte von Vektoren, also gerichteten Strecken mit Anfangs-
und Endpunkt zu betrachten. Einen Vektor vom Ursprung eines
Koordinatensystems nach einem Punkt A bezeichnet man als
Ortsvektor
![]() und schreibt
und schreibt
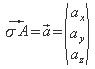 oder
oder
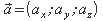 ,
,
wobei ax, ay
und az die Koordinaten des Punktes A
sind.
Eine Vergrößerung oder Verkleinerung eines Objektes ergibt sich, wenn einfach jede Komponente aller Ortsvektoren mit einem Faktor multipliziert wird. Dies geschieht in unserem Programm (Listing 1), um die Größe des Modells zu definieren.
Soll der Körper verschoben werden, so wird zu
jedem Ortsvektor ein konstanter Verschiebungsvektor addiert. Wenn
schließlich eine Drehung ausgeführt werden soll, so
entspricht dies einer Multiplikation der Ortsvektoren mit einer
sogenannten Rotationsmatrix. Dazu sei nur Folgendes erklärt:
Eine Drehung um eine beliebige Achse läßt sich in eine Drehung
um die x-, y- und z-Achse und eine anschließende Verschiebung
zerlegen. Die Rotationsmatrizen dafür haben die Form
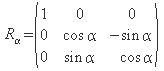
Drehung mit α um die x-Achse
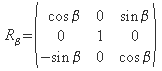
Drehung mit β um die y-Achse
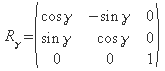
Drehung mit γ um die z-Achse
Ein gedrehter Ortsvektor
![]() ergibt sich im allgemeinsten Fall durch Verknüpfung aller
Rotationen:
ergibt sich im allgemeinsten Fall durch Verknüpfung aller
Rotationen:
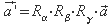
Für die erforderlichen Rechenregeln mit Matrizen und Vektoren sei wieder auf die Literatur verwiesen.
In unserem Programm lassen sich 3D-Modelle wie im Bild gezeigt nur um die x- und z-Achse drehen. Eine Verschiebung sowie eine Größenänderung findet nur einmal am Anfang statt, um das Objekt an die Grafikauflösung anzupassen.
Projektionsformen
Nun stellt sich noch das Problem, das Objekt auf
den Bildschirm zu projizieren. Hier unterscheidet man zwischen
Parallel- und Zentralprojektion. Die Zentralprojektion entspricht
etwa dem menschlichen Sehen, die Parallelprojektion ist eher eine
mathematische Form, die den Vorteil des geringen Rechenaufwandes
besitzt. Zunächst die Zentralprojektion: Von einem Zentralpunkt
Z (mit Ortsvektor
![]() aus verbindet man jeden Körperpunkt A mit einem Bildpunkt
B auf einer Ebene. Die Schreibweise ist
aus verbindet man jeden Körperpunkt A mit einem Bildpunkt
B auf einer Ebene. Die Schreibweise ist
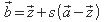
wobei die Zahl s Streckungsfaktor heißt.
Im konkreten Fall einer Projektion auf die
x,z-Ebene ergibt das in Matrizenschreibweise
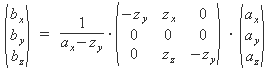
Bei der Parallelprojektion entfällt der
Zentralpunkt. Die Schreibweise lautet nun
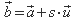 ;
;
wobei
![]() als Projektionsvektor bezeichnet wird.
als Projektionsvektor bezeichnet wird.
Setzt man
![]() = (0;1;0), so reduziert sich die Berechnung des Bildpunktes auf die
Zuordnung
= (0;1;0), so reduziert sich die Berechnung des Bildpunktes auf die
Zuordnung
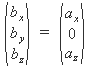
Das Programm bietet beide Projektionsarten an. Gedreht wird mit den Cursortasten, dabei ist die Zuordnung in Parallelprojektion nicht eindeutig, da hier „vorne“ und „hinten“ nicht unterscheidbar sind und vom Betrachter abhängen.
Der Name des Drahtmodells wird beim Programmaufruf als Parameter angegeben (zum Beispiel DREHEN QUADER.3DV). Der Suchpfad für den BGI-Treiber wird in der Environment-Variablen „BGI“; definiert. Diese Definition kann in der AUTOEXEC.BAT erfolgen (z.B. set BGI=C:\TP6\TREIBER). Derart compilierte Programme können bei einer Änderung der Verzeichnisstruktur unverändert übernommen werden, lediglich der Eintrag in der AUTOEXEC.BAT muß angepaßt werden.
Bezüglich der Grafikkarte wird eine Standard-VGA (oder EGA-Karte) mit 256 KByte RAM erwartet. Als Modus wird eine Auflösung von 640×350 Punkten benutzt, da dies die höchste Auflösung ist, bei der zwei Videoseiten verwendet werden können. Mehrere Videoseiten lassen sich zwar grundsätzlich auch in höherauflösenden Modi programmieren, aber nur mittels besonderer BGI-Treiber und kartenspezifischer Ansteuerungen (siehe [2]).
Das Schalten zwischen Videoseiten, auch Video-Swapping genannt, ist ein Clou des Programms. Es gewährleistet eine einfache Art der möglichst flackerfreien Darstellung von Bewegungen: Während das alte Bild auf dem Bildschirm angezeigt wird, wird im Hintergrund das neue Bild aufgebaut. Ist dieses fertig, entsteht beim Umschalten auf die Videoseite des neuen Bildes der Eindruck einer schlagartig auf den Bildschirm gebrachten Grafik. Der Betrachter sieht das eigentliche Zeichnen gar nicht und hat durch permanentes Schalten zwischen den zwei Videoseiten den Eindruck einer fließenden Bewegung.
Die Geschwindigkeit der Drehung eines Objekts ist natürlich abhängig von der Rechenzeit für eine Seite. Der Quotient aus Anzahl der Punkte für das Objekt und der Rechenleistung des PC sollte also möglichst klein gehalten werden. Die Anzahl der möglichen Punkte und Linien ist derzeit willkürlich auf 500 beziehungsweise 1000 beschränkt, kann aber bei Bedarf auch geändert werden.
Das Datenformat der 3D-Dateien
Die Informationen der Drahtmodelle sind in einer ASCII-Datei abgelegt. In der ersten Zeile wird die Anzahl der verwendeten Punkte angegeben. Bei dem Quader aus Listing 2 sind dies acht. Danach folgen für jeden dieser Punkte die x-, y-, und z-Koordinaten, die immer eine Zeile beanspruchen. Der nächste Dateieintrag bestimmt die Zahl der Linien, die die einzelnen, vorher definierten Punkte verbinden. Die restlichen Zeilen enthalten jeweils die Angabe des Punktes, der angesteuert wird und die Farbe, die die entsprechende Verbindungslinie bekommen soll. Falls an dieser Stelle die Farbe 0 steht, bedeutet das bei schwarzem Hintergrund eine unsichtbare Linie, also lediglich eine Bewegung. Dieses etwas merkwürdige Datenformat gestattet es, mit einem normalen Texteditor neue Drahtmodelle zu entwerfen. Der Quader aus Listing 2 eignet sich sehr gut, das Dateiformat nachzuvollziehen, da für jede seiner Kanten eine andere Farbe verwendet wurde. Die restlichen 3D-Modelle (Listing 3 und 4), stammen von Oscar Garcia aus Neuseeland.
Wer sich weiter mit derart bewegter Grafik beschäftigten möchte, dem seien hier noch ein paar Tips mit auf den Weg gegeben: Durch eine gute Fallunterscheidung (zum Beispiel reine x-, y- oder z-Rotation) können etliche Rechenoperationen vermieden werden. Besonders trigonometrische Berechnungen und Multiplikationen gilt es zu vermeiden. Ebenfalls beschleunigend wirkt die Verwendung von Integer- statt Real-Zahlen. Und nicht zuletzt ist die Grafik oft der Flaschenhals. Hier wirken Assemblerroutinen mitunter wahre Wunder, aber auch schnelle BGI-Treiber sind schon mehrfach veröffentlicht worden und liefern gute Dienste.
Horst Scheid/bs
Literatur
Listing 1. Das Turbo-Pascal-Programm zum Drehen von Objekten
program drehen;
(********************************************
* 3D-Programm zum Drehen von Drahtmodellen *
* Autor : Horst Scheid *
* Datum : 31.5.92 *
* Compiler : Turbo Pascal 4/5.x/6.0 *
*********************************************)
{$ifdef CPU87} (* Coprozessor da ? *)
{$N+}
{$else}
{$N-}
{$endif}
uses dos,crt,graph;
{$ifdef CPU87}
type real=extended;
{$endif}
const anzp = 500; (* maximale Punktzahl *)
anzl = 1000; (* maximale Linienzahl *)
mx = 320; (* x-Offset *)
my = 150; (* y-Offset *)
scal = 150; (* Skalierungsfaktor *)
type tupel = record
x,y,z : integer;
end;
rtupel = record
x,y,z : real;
end;
var p : array[0..anzp,1..3] of real;
pk,pd : array[0..anzp] of rtupel;
l : array[0..anzl,0..1] of integer;
f : text;
s : string;
a : shortint;
ap : tupel;
rp,rm,dp,dm : array[1..3,1..3] of real;
al,be,ga,max : real;
m : array[1..3] of real;
c : char;
i,j,k,e,np,nl : integer;
alfa,gamma : integer;
procedure def; (* Initialisierungen *)
var i:integer;
begin
ap.x:=220;
ap.y:=220;
ap.z:=220;
al:=0;
be:=0;
ga:=0;
end;
procedure dreh_m;
(* Berechnung von Zwischengrößen spart Zeit *)
var x,y,u,v : real;
begin
x:=sin(ga); (* trigonometrische Funktionen *)
y:=cos(al);
u:=sin(al);
v:=cos(ga);
rp[1,1]:=v; (* Komponenten der Drehmatrix *)
rp[2,1]:=x;
rp[3,1]:=0;
rp[1,2]:=y*x;
rp[2,2]:=y*v;
rp[3,2]:=-u;
rp[1,3]:=u*x;
rp[2,3]:=u*v;
rp[3,3]:=y;
end;
procedure dreh(var x:rtupel);
(* eigentliche Drehung um zwei Achsen *)
var temp : rtupel;
begin
temp.x:=x.x*rp[1,1]+x.y*rp[1,2]+x.z*rp[1,3];
temp.y:=x.x*rp[2,1]+x.y*rp[2,2]+x.z*rp[2,3];
temp.z:=x.y*rp[3,2]+x.z*rp[3,3];
(* x.x*rp[3,1] entfällt, da =0 *)
x:=temp;
end;
procedure c_line(k:rtupel);
(* Zentralprojektion auf die x,z-Ebene *)
var x,y : integer;
f : real;
begin
f:=(k.y-ap.y);
if f=0 then exit;
(* Vorsicht mit der Skalierung ! *)
x:=round((ap.x*k.y-ap.y*k.x)/f)+mx;
y:=round((ap.y*k.y-ap.y*k.z)/f)+my;
lineto(x,y);
end;
procedure p_line(k:rtupel);
(* Parallelprojektion mit Vektor (0;0;1) *)
begin
lineto(round(k.x)+mx,-round(k.z)+my);
end;
procedure init;
(* initialisierung der Grafik *)
var gd,gm :integer;
begin
gd:=9 (* VGA *);
gm:=1 (* 640*350 Pixel *);
initgraph(gd,gm,getenv('BGI'));
(* Environment definieren, siehe Text ! *)
a:=1;
end;
procedure lesen;
begin
{$I-}
reset(f);
{$I+}
if ioresult<>0 then begin
writeln('File error');
halt(0);
end;
readln(f,s);
val(s,np,e);
if e<>0 then val(copy(s,1,e-1),np,e);
writeln('lese File-Daten ...');
for i:=1 to np do begin
readln(f,s);
val(s,p[i,1],e);
val(copy(s,1,e-1),p[i,1],j);
delete(s,1,e);
val(s,p[i,2],e);
val(copy(s,1,e-1),p[i,2],j);
delete(s,1,e);
val(s,p[i,3],e);
if e<>0 then val(copy(s,1,e-1),p[i,3],e);
end;
readln(f,s);
val(s,nl,e);
if e<>0 then val(copy(s,1,e-1),nl,e);
for i:=1 to nl do begin
readln(f,s);
val(s,l[i,0],e);
val(copy(s,1,e-1),l[i,0],j);
delete(s,1,e);
val(s,l[i,1],e);
if e<>0 then val(copy(s,1,e-1),l[i,1],e);
end;
close(f);
end;
begin
def;
for i:=0 to anzp do
for j:=1 to 3 do p[i,j]:=0;
for i:=0 to anzl do
for j:=0 to 1 do l[i,j]:=0;
if paramcount=1 then assign(f,paramstr(1))
else begin writeln('3d-Datei nicht angeben');
halt(0);
end;
lesen;
writeln('konvertiere Daten ....');
max:=0;
for i:=1 to np do
for j:=1 to 3 do
if abs(p[i,j])>max then max:=abs(p[i,j]);
for i:=1 to np do
for j:=1 to 3 do p[i,j]:=p[i,j]/max;
for i:=1 to 3 do m[i]:=0;
for i:=1 to np do
for j:=1 to 3 do m[j]:=m[j]+p[i,j];
for i:=1 to 3 do m[i]:=m[i]/np;
for i:=1 to np do
begin pk[i].x:=round((p[i,1]-m[1])*scal);
pk[i].y:=round((p[i,2]-m[2])*scal);
pk[i].z:=round((p[i,3]-m[3])*scal);
end;
init;
setcolor(15);
setactivepage(0);
setvisualpage(0);
outtextxy(1,320,'Cursor-Tasten - drehen');
outtextxy(300,320,'ESC - beenden');
outtextxy(500,320,'Seite : 1');
setactivepage(1);
setvisualpage(1);
outtextxy(1,320,'Cursor-Tasten - drehen');
outtextxy(300,320,'ESC - beenden');
outtextxy(500,320,'Seite : 2');
setviewport(0,0,639,300,clipon);
c:=' ';
alfa:=0;
gamma:=0;
dreh_m;
while c<>#27 do begin
setvisualpage(a);
if a=1 then a:=0
else a:=1;
setactivepage(a);
clearviewport;
if keypressed then begin
c:=readkey;
if c=#00 then c:=readkey;
case c of '8',#72 : inc(alfa,3);
'2',#80 : dec(alfa,3);
'6',#75 : inc(gamma,3);
'4',#77 : dec(gamma,3);
end;
al:=alfa*pi/180; (* Bogenmaß *)
ga:=gamma*pi/180; (* Bogenmaß *)
dreh_m;
end;
pd:=pk;
(* jetzt alle Vektoren drehen ... *)
for i:=1 to np do dreh(pd[i]);
(* ... und anschließend projezieren *)
for i:=1 to nl do begin
setcolor(l[i,1]);
p_line(pd[l[i,0]]);
(* p_line = parallel, c_line = zentral *)
end;
end;
closegraph;
end.
Listing 2. Abtippen uns als Textfile speichern:
Diese Daten ergeben einen Quader
8
-7.5 0 7.5
-7.5 10 7.5
7.5 10 7.5
7.5 0 7.5
-7.5 0 -7.5
-7.5 10 -7.5
7.5 10 -7.5
7.5 0 -7.5
17
1 0
2 1
3 2
4 3
1 4
5 0
6 6
7 7
8 8
5 9
1 12
6 0
2 13
7 0
3 14
8 0
4 15
Listing 3. Streng geheim: Die Daten dieses
Listings ergebenmit dem ‚drehen’-Programm
ein interessantes Objekt
50
1 1 1
1 -1 -1
-1 1 -1
-1 -1 1
-1.5 3.5 3.5
-1.5 3.5 1.5
-1.5 1.5 3.5
-1.5 1.5 1.5
-3.5 3.5 3.5
-3.5 3.5 1.5
-3.5 1.5 3.5
-3.5 1.5 1.5
3.5 2.5 -2.5
1.5 2.5 -2.5
2.5 3.5 -2.5
2.5 1.5 -2.5
2.5 2.5 -1.5
2.5 2.5 -3.5
3.5 -1.5 3.5
3.5 -1.5 1.5
3.5 -3.5 3.5
3.5 -3.5 1.5
1.5 -1.5 3.5
1.5 -1.5 1.5
1.5 -3.5 3.5
1.5 -3.5 1.5
3.118034 -0.881966 2.5
1.881966 -0.881966 2.5
3.118034 -4.118034 2.5
1.881966 -4.118034 2.5
4.118034 -2.5 3.118034
4.118034 -2.5 1.881966
0.881966 -2.5 3.118034
0.881966 -2.5 1.881966
2.5 -1.881966 4.118034
2.5 -3.118034 4.118034
2.5 -1.881966 0.881966
2.5 -3.118034 0.881966
-0.881966 -1.5 -2.5
-4.118034 -1.5 -2.5
-0.881966 -3.5 -2.5
-4.118034 -3.5 -2.5
-1.5 -2.5 -0.881966
-1.5 -2.5 -4.118034
-3.5 -2.5 -0.881966
-3.5 -2.5 -4.118034
-2.5 -0.881966 -1.5
-2.5 -4.118034 -1.5
-2.5 -0.881966 -3.5
-2.5 -4.118034 -3.5
114
4 0
3 14
2 14
1 14
4 14
2 14
1 0
3 14
6 0
5 12
7 12
8 12
6 12
10 12
9 12
11 12
12 12
10 12
5 0
9 12
7 0
11 12
8 0
12 12
13 0
15 9
14 9
17 9
16 9
18 9
13 9
16 9
14 9
18 9
15 9
17 9
13 9
19 0
27 15
20 15
32 15
31 15
19 15
35 0
36 15
21 15
31 15
21 0
29 15
22 15
32 15
20 0
37 15
24 15
34 15
26 15
38 15
22 15
37 0
38 15
19 0
35 15
23 15
33 15
25 15
36 15
23 0
28 15
24 15
28 0
27 15
25 0
30 15
26 15
29 0
30 15
33 0
34 15
39 0
47 10
43 10
39 10
44 10
49 10
39 10
41 10
43 10
45 10
47 10
49 10
46 10
44 10
41 10
48 10
43 10
42 0
45 10
48 10
42 10
50 10
48 10
41 0
50 10
44 10
50 0
46 10
42 10
40 10
45 10
46 0
40 10
47 10
49 0
40 10
Listing 4. Viel Tipparbeit, dafür
entschädigt das entstehende Objekt
264
.75818 .50000 .04045
.73586 .60501 .04045
.67276 .69187 .04045
.57978 .74555 .04045
.47301 .75677 .04045
.37091 .72359 .04045
.29113 .65176 .04045
.24746 .55368 .04045
.24746 .44632 .04045
.29113 .34824 .04045
.37091 .27641 .04045
.47301 .24323 .04045
.57978 .25445 .04045
.67276 .30813 .04045
.73586 .39499 .04045
.75818 .50000 .04045
.65534 .50000 .04308
.64191 .56318 .04308
.60394 .61544 .04308
.54800 .64773 .04308
.48376 .65449 .04308
.42233 .63453 .04308
.37433 .59130 .04308
.34806 .53230 .04308
.34806 .46770 .04308
.37433 .40870 .04308
.42233 .36547 .04308
.48376 .34551 .04308
.54800 .35227 .04308
.60394 .38456 .04308
.64191 .43682 .04308
.65534 .50000 .04308
.59643 .50000 .06219
.58810 .53922 .06219
.56453 .57166 .06219
.52980 .59171 .06219
.48992 .59590 .06219
.45178 .58351 .06219
.42198 .55668 .06219
.40567 .52005 .06219
.40567 .47995 .06219
.42198 .44332 .06219
.45178 .41649 .06219
.48992 .40410 .06219
.52980 .40829 .06219
.56453 .42834 .06219
.58810 .46078 .06219
.59643 .50000 .06219
.56277 .50000 .10697
.55734 .52553 .10697
.54200 .54665 .10697
.51940 .55970 .10697
.49344 .56243 .10697
.46861 .55436 .10697
.44922 .53690 .10697
.43860 .51305 .10697
.43860 .48695 .10697
.44922 .46310 .10697
.46861 .44564 .10697
.49344 .43757 .10697
.51940 .44030 .10697
.54200 .45335 .10697
.55734 .47447 .10697
.56277 .50000 .10697
.54481 .50000 .17324
.54094 .51823 .17324
.52999 .53330 .17324
.51385 .54262 .17324
.49532 .54457 .17324
.47759 .53881 .17324
.46375 .52634 .17324
.45617 .50932 .17324
.45617 .49068 .17324
.46375 .47366 .17324
.47759 .46119 .17324
.49532 .45543 .17324
.51385 .45738 .17324
.52999 .46670 .17324
.54094 .48177 .17324
.54481 .50000 .17324
.53826 .50000 .24898
.53495 .51556 .24898
.52560 .52843 .24898
.51182 .53638 .24898
.49600 .53805 .24898
.48087 .53313 .24898
.46905 .52249 .24898
.46258 .50795 .24898
.46258 .49205 .24898
.46905 .47751 .24898
.48087 .46687 .24898
.49600 .46195 .24898
.51182 .46362 .24898
.52560 .47157 .24898
.53495 .48444 .24898
.53826 .50000 .24898
.54199 .50000 .32195
.53836 .51708 .32195
.52810 .53121 .32195
.51298 .53994 .32195
.49561 .54176 .32195
.47900 .53637 .32195
.46603 .52468 .32195
.45892 .50873 .32195
.45892 .49127 .32195
.46603 .47532 .32195
.47900 .46363 .32195
.49561 .45824 .32195
.51298 .46006 .32195
.52810 .46879 .32195
.53836 .48292 .32195
.54199 .50000 .32195
.55681 .50000 .38461
.55190 .52311 .38461
.53802 .54222 .38461
.51756 .55403 .38461
.49406 .55650 .38461
.47159 .54920 .38461
.45404 .53339 .38461
.44443 .51181 .38461
.44443 .48819 .38461
.45404 .46661 .38461
.47159 .45080 .38461
.49406 .44350 .38461
.51756 .44597 .38461
.53802 .45778 .38461
.55190 .47689 .38461
.55681 .50000 .38461
.58410 .50000 .43555
.57683 .53421 .43555
.55627 .56250 .43555
.52599 .57998 .43555
.49121 .58364 .43555
.45795 .57283 .43555
.43196 .54943 .43555
.41774 .51749 .43555
.41774 .48251 .43555
.43196 .45057 .43555
.45795 .42717 .43555
.49121 .41636 .43555
.52599 .42002 .43555
.55627 .43750 .43555
.57683 .46579 .43555
.58410 .50000 .43555
.62421 .50000 .47882
.61347 .55052 .47882
.58311 .59231 .47882
.53838 .61813 .47882
.48702 .62353 .47882
.43789 .60757 .47882
.39951 .57301 .47882
.37850 .52583 .47882
.37850 .47417 .47882
.39951 .42699 .47882
.43789 .39243 .47882
.48702 .37647 .47882
.53838 .38187 .47882
.58311 .40769 .47882
.61347 .44948 .47882
.62421 .50000 .47882
.67472 .50000 .52232
.65961 .57107 .52232
.61691 .62984 .52232
.55399 .66617 .52232
.48174 .67376 .52232
.41264 .65131 .52232
.35865 .60270 .52232
.32910 .53633 .52232
.32910 .46367 .52232
.35865 .39730 .52232
.41264 .34869 .52232
.48174 .32624 .52232
.55399 .33383 .52232
.61691 .37016 .52232
.65961 .42894 .52232
.67472 .50000 .52232
.72913 .50000 .57612
.70932 .59320 .57612
.65332 .67028 .57612
.57081 .71792 .57612
.47605 .72788 .57612
.38543 .69843 .57612
.31463 .63468 .57612
.27588 .54764 .57612
.27588 .45236 .57612
.31463 .36532 .57612
.38543 .30157 .57612
.47605 .27212 .57612
.57081 .28208 .57612
.65332 .32972 .57612
.70932 .40680 .57612
.72913 .50000 .57612
.77710 .50000 .65002
.75314 .61270 .65002
.68541 .70592 .65002
.58563 .76353 .65002
.47104 .77558 .65002
.36145 .73997 .65002
.27583 .66287 .65002
.22896 .55761 .65002
.22896 .44239 .65002
.27583 .33713 .65002
.36145 .26003 .65002
.47104 .22442 .65002
.58563 .23647 .65002
.68541 .29408 .65002
.75314 .38730 .65002
.77710 .50000 .65002
.80689 .50000 .74899
.78036 .62482 .74899
.70535 .72806 .74899
.59483 .79187 .74899
.46792 .80521 .74899
.34656 .76577 .74899
.25172 .68038 .74899
.19982 .56381 .74899
.19982 .43619 .74899
.25172 .31962 .74899
.34656 .23423 .74899
.46792 .19479 .74899
.59483 .20813 .74899
.70535 .27194 .74899
.78036 .37518 .74899
.80689 .50000 .74899
.80992 .50000 .86395
.78313 .62606 .86395
.70738 .73032 .86395
.59577 .79475 .86395
.46760 .80822 .86395
.34504 .76840 .86395
.24927 .68217 .86395
.19685 .56444 .86395
.19685 .43556 .86395
.24927 .31783 .86395
.34504 .23160 .86395
.46760 .19178 .86395
.59577 .20525 .86395
.70738 .26968 .86395
.78313 .37394 .86395
.80992 .50000 .86395
.78455 .50000 .95500
.75995 .61574 .95500
.69040 .71146 .95500
.58793 .77062 .95500
.47026 .78299 .95500
.35773 .74642 .95500
.26980 .66725 .95500
.22167 .55916 .95500
.22167 .44084 .95500
.26980 .33275 .95500
.35773 .25358 .95500
.47026 .21701 .95500
.58793 .22938 .95500
.69040 .28854 .95500
.75995 .38427 .95500
.78455 .50000 .95500
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
272
1 0
2 9
3 9
4 9
5 9
6 9
7 9
8 9
9 9
10 9
11 9
12 9
13 9
14 9
15 9
16 9
17 0
18 9
19 9
20 9
21 9
22 9
23 9
24 9
25 9
26 9
27 9
28 9
29 9
30 9
31 9
32 9
33 0
34 9
35 9
36 9
37 9
38 9
39 9
40 9
41 9
42 9
43 9
44 9
45 9
46 9
47 9
48 9
49 0
50 9
51 9
52 9
53 9
54 9
55 9
56 9
57 9
58 9
59 9
60 9
61 9
62 9
63 9
64 9
65 0
66 9
67 9
68 9
69 9
70 9
71 9
72 9
73 9
74 9
75 9
76 9
77 9
78 9
79 9
80 9
81 0
82 9
83 9
84 9
85 9
86 9
87 9
88 9
89 9
90 9
91 9
92 9
93 9
94 9
95 9
96 9
97 0
98 9
99 9
100 9
101 9
102 9
103 9
104 9
105 9
106 9
107 9
108 9
109 9
110 9
111 9
112 9
113 0
114 9
115 9
116 9
117 9
118 9
119 9
120 9
121 9
122 9
123 9
124 9
125 9
126 9
127 9
128 9
129 0
130 9
131 9
132 9
133 9
134 9
135 9
136 9
137 9
138 9
139 9
140 9
141 9
142 9
143 9
144 9
145 0
146 9
147 9
148 9
149 9
150 9
151 9
152 9
153 9
154 9
155 9
156 9
157 9
158 9
159 9
160 9
161 0
162 9
163 9
164 9
165 9
166 9
167 9
168 9
169 9
170 9
171 9
172 9
173 9
174 9
175 9
176 9
177 0
178 9
179 9
180 9
181 9
182 9
183 9
184 9
185 9
186 9
187 9
188 9
189 9
190 9
191 9
192 9
193 0
194 9
195 9
196 9
197 9
198 9
199 9
200 9
201 9
202 9
203 9
204 9
205 9
206 9
207 9
208 9
209 0
210 9
211 9
212 9
213 9
214 9
215 9
216 9
217 9
218 9
219 9
220 9
221 9
222 9
223 9
224 9
225 0
226 9
227 9
228 9
229 9
230 9
231 9
232 9
233 9
234 9
235 9
236 9
237 9
238 9
239 9
240 9
241 0
242 9
243 9
244 9
245 9
246 9
247 9
248 9
249 9
250 9
251 9
252 9
253 9
254 9
255 9
256 9
257 0
258 7
262 7
261 7
263 7
264 7
260 7
259 7
257 7
261 7
262 0
264 7
258 0
260 7
259 0
263 7aus mc 08/92 – Seite 110-113
