Artikel
Lichtblick
Alles über die bunte Welt der Farbmodelle
Erst die Farbe macht aus der PC-Grafik eine angenehm anzuschauende Sache. Dies gilt besonders für die Game-Freunde. Doch trotz der in den letzten Jahren stetig weiterentwickelten Technik sind selbst die besten Grafikkarten und Monitore noch weit von der Wirklichkeit der 350000 Farben entfernt, die das menschliche Auge mühelos unterscheiden kann. Hier ein kompakter Einblick in die Farbtheorie.
Wissenschaftler haben
schon frühzeitig begonnen, Systeme zur möglichst
eindeutigen Beschreibung von Farben zu entwickeln. Im Laufe der Zeit
haben sich mehrere Standardmodelle herausgebildet. Basis ist
natürlich das menschliche Auge und die Erkenntnisse der Physik
über das Licht.
Für das eigentliche Farbempfinden sind drei
Parameter wichtig: Die dominante Wellenlänge, deren Sättigung
und deren Intensität. Die dominante Wellenlänge des Lichts,
die von einem Objekt ausgesendet oder reflektiert wird, entspricht
dem, was wir gemeinhin als Farbe bezeichnen. Eine exakte Messung kann
es in diesem Bereich jedoch nicht geben. So wird beispielsweise Rot
in einem Wellenlängenbereich um 630 nm
und Blau im Bereich von 450 bis 480 nm
erkannt. Da der gesamte Spektralbereich mal gerade 400 nm
umfaßt, sind die 30 nm,
in dem Blau erkannt wird, ein recht großes Intervall von
fast 10 Prozent, aber Farbempfinden ist nun einmal subjektiv.
Ähnlich ist es mit der Sättigung der
Farbe. Darunter versteht man die Bündelung des Lichts oder die
Anzahl der unterschiedlichen Wellenlängen. Je kleiner der
Wellenlängenbereich ist, desto reiner erscheint die Farbe und je
größer der Wellenlängenbereich, desto geringer ist
die Reinheit.
Die Helligkeit läßt sich mit der
Intensität oder der Energie des Lichtes gleichsetzen. Je größer
die Intensität, desto größer die Helligkeit.
Interessant wird es, wenn mehrere
verschiedenartige Lichtquellen zusammentreffen. Dann entstehen
Mischfarben, die sich natürlich auch gezielt hervorrufen lassen.
Den Sonderfall, daß zwei Farben zusammen weiß ergeben,
nennt man Komplementärfarben. Mit Hilfe geeigneter Basisfarben
lassen sich beliebige Farbpaletten mischen. Diese werden
üblicherweise Grund- oder Primärfarben genannt.
Die richtige Mixtur bringts
Eine Grundmenge von Primärfarben, aus denen sich alle anderen Farben mischen lassen, gibt es nicht. Es existiert darum seit 1931 ein Modell, mit dem sich jede Farbe als Summe dreier willkürlich gewählter Grundfarben beschreiben läßt. In diesem nach der Commission Internationale de l'Éclairage benannten CIE-Farbmodell (Bild 1) wird jede Grundfarbe durch ihre Energieverteilungskurve charakterisiert. Die Werte auf der Kurve entsprechen den Wellenlängen in nm (Nanometer). Die Koordinaten des CIE-Farbdiagramms ermöglichen die exakte Beschreibung von Farben und ihren Austausch zwischen Systemen mit verschiedenen Primärfarben. So entsprechen beispielsweise die RGB-Grundfarben, die meist für Computermonitore als Primärfarben verwendet werden, den CIE-Koordinaten Rot = (0,628 und 0,346), Grün = (0,268 und 0,588) und Blau = (0,150 und 0,070).
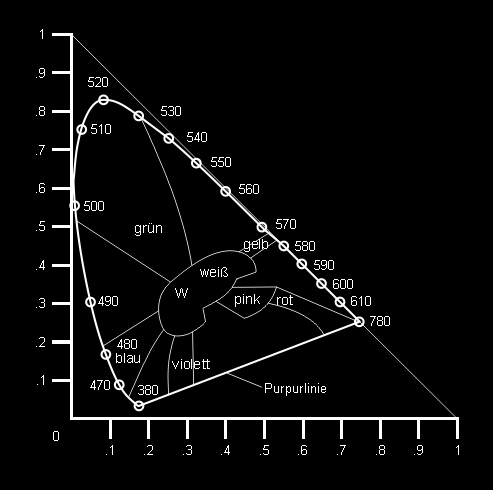
- Bild 1. In dem CIE-Farbmodell wird jede Grundfarbe durch ihre Energieverteilungskurve charakterisiert. Die Werte auf der Kurve entsprechen den Wellenlängen in nm.
In der Computertechnik hat man sich schon sehr
frühzeitig dazu entschieden, sich dem Auge anzupassen. Die
meisten Farbmonitore verwenden deshalb roten, grünen und blauen
Phosphor, und das Mischen von Farben auf Basis dieser Primärfarben
ist das derzeit meist verbreitete Farbmodell, das beispielsweise auch
von Microsoft Windows verwendet wird.
Das RGB-Farbmodell (Bild 2)
kombiniert die drei Grundfarben in einem dreidimensionalen Koordinatensystem von der
Form eines Würfels. Jede Farbe wird als Zahlentripel
(R, G, B)
dargestellt. Schwarz wird als das Fehlen jeder Farbe aufgefaßt,
was zum Tripel (0, 0, 0) führt, während Weiß mit (1, 1, 1)
codiert wird. Aufgrund dieser Eigenschaft bezeichnet man das
RGB-Farbmodell auch als additives Modell, da Mischfarben durch das
Addieren von Grundfarben entstehen. So ist Gelb beispielsweise (1, 1, 0).
Für die Primärfarben ergibt sich:
Rot = (1, 0, 0),
Grün = (0, 1, 0),
Blau = (0, 0, 1).
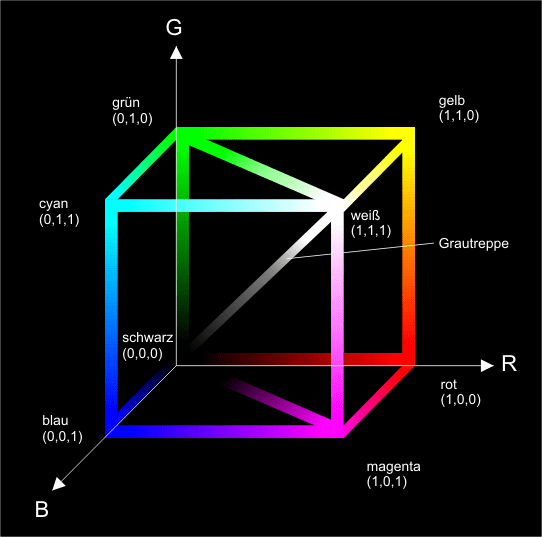
- Bild 2. Das RGB-Farbmodell kombiniert die drei Grundfarben in einem dreidimensionalen Koordinatensystem. Jede Farbe wird als Zahlentripel (R, G, B) dargestellt.
Im RGB-Farbmodell
sind alle Koordinatenachsen auf 1 normiert. Die meisten Programme
setzen jedoch einen Bereich von 0 bis 255 voraus, der logisch auf den Bereich
von 0 bis 1 abgebildet werden muß, damit er dem
RGB-Modell entspricht. Auch die im
Rahmen dieses Beitrags vorgestellten Routinen erwarten Werte zwischen
0 und 1. Eine Umrechnung von logischen Werten in reale kann jedoch
einfach durch Division mit 255 erfolgen. Beispiel:
Mischfarbe = (170, 255, 170),
RGB-Wert = (170/255, 1, 170/255).
Eine Variante des RGB-Farbmodells
ist das Umdrehen der Hauptdiagonalen, die von Schwarz nach Weiß zeigt.
Daraus entsteht das Cyan-Magenta-Gelb-Mischmodell
(CMY,
Bild 3),
das Hauptfarben subtrahiert, anstatt zu addieren. Den gewünschten
Farbeffekt erzielt man, indem Farben vom weißen Licht abgezogen werden.
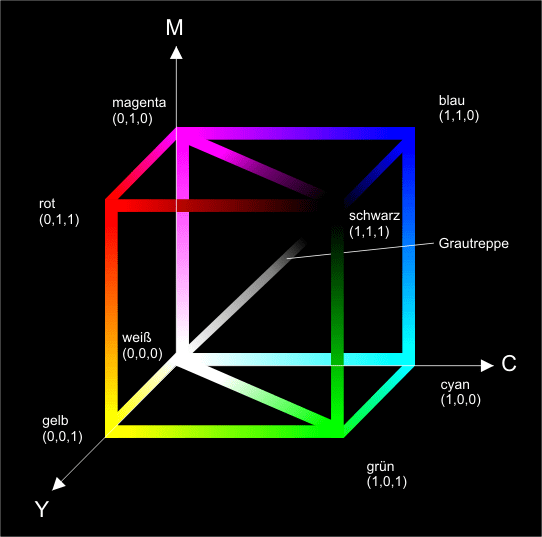
- Bild 3. Eine Variante des RGB-Farbmodells ist das Umdrehen der Hauptdiagonalen, die von Schwarz nach Weiß zeigt. Daraus entsteht das Cyan-Magenta-Gelb-Mischmodell, das Hauptfarben subtrahiert, anstatt zu addieren.
Wie auch beim RGB-Farbmodell liegen auf der
Diagonalen von Weiß nach Schwarz die Grauwerte. Diese ergeben
sich immer als gleichmäßige Bestandteile aller
Grundfarben. Dies ist auch nicht weiter verwunderlich, denn wenn die
Koordinaten (0, 0, 0) Schwarz und (1, 1, 1) Weiß sind, dann muß
(0.5, 0.5, 0.5) ein Mittel zwischen Schwarz und Weiß sein, in
dem keine Primärfarbe dominiert oder unterrepräsentiert
ist. Folglich ergibt sich ein Grauwert.
RGB- und CMY-Farbmodell stehen in einer simplen
Beziehung zueinander:
Cyan = 1 − Rot,
Magenta = 1 − Grün,
Gelb = 1 − Blau.
Über diese Formel lassen sich die Werte einfach umrechnen.
In dem 1953 in den USA eingeführten
NTSC-Fernsehsystem
werden die Farben durch die Farbparameter
YIQ
beschrieben. Auch das YIQ-Farbmodell
wird durch ein dreidimensionales Koordinatensystem definiert.
Die Y Komponente des Modells stellt eine Grundfarbe dar,
deren spektrale Energieverteilung der Helligkeitskurve entspricht, wobei die
Y Komponente äquivalent zur definierten
Farbe ist. Etwas weniger kompliziert ausgedrückt: Die Y Komponente
entspricht der Y Koordinate im
CIE-Farbenraum.
Der wichtigste Vorteil des YIQ-Farbmodells
gegenüber dem RGB- und
CMY-Modell
besteht darin, daß mit YIQ
die Umsetzung der unterschiedlichen Farben auf entsprechend unterschiedliche Intensitätsgrade
gelöst wird, während im RGB-Modell
zwei verschiedene Schattierungen durchaus die gleiche Helligkeit erzeugen können.
Genau dies ist jedoch ein wichtiger Aspekt, wenn ein ausgestrahltes Bild sowohl auf Farb-
wie auch auf Schwarzweißfernsehern gut empfangen werden soll. Die europäische
PAL-Norm arbeitet
ähnlich, jedoch werden hier in den Parametern I
und Q die Farbdifferenzen
R-Y und
B-Y übertragen.
Die Umrechnung von RGB nach
YIQ
und umgekehrt erfolgt über eine Matrizenmultiplikation:
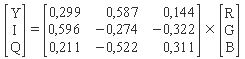
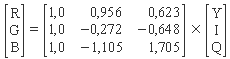
Allen bisher besprochenen Farbmodellen ist gemein,
daß sie sich an der Hardware orientieren oder versuchen, das
Auge zu simulieren. Anstelle der Angabe der Rot-, Grün- und
Blau-Farbanteile kann eine Farbe jedoch auch über ihre Parameter
Farbton, Helligkeit und Reinheit beschrieben werden. Exakt diesen Weg
beschreitet das HSV-Modell,
das die Parameter Hue (Farbe),
Saturation (Sättigung, Reinheit)
und Value (Helligkeit) verwendet.
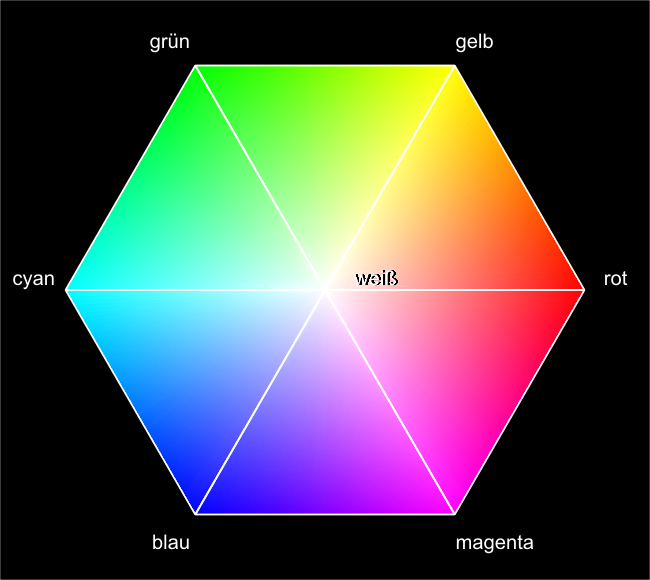
Den typischen HSV-Hexakegel
(Bild 4) erhält
man, indem man den RGB-Einheitswürfel
entlang der Diagonalen von Schwarz nach Weiß projiziert. Es resultiert ein Sechseck, das
die Basis der HSV-Pyramide
bildet. Jede Farbe wird durch einen Winkel in diesem Sechseck angegeben,
wobei Rot mit dem Winkel 0 den Anfang macht. Komplementärfarben liegen jeweils
180 Grad auseinander. H kann somit Werte zwischen
0 und 360 Grad annehmen.
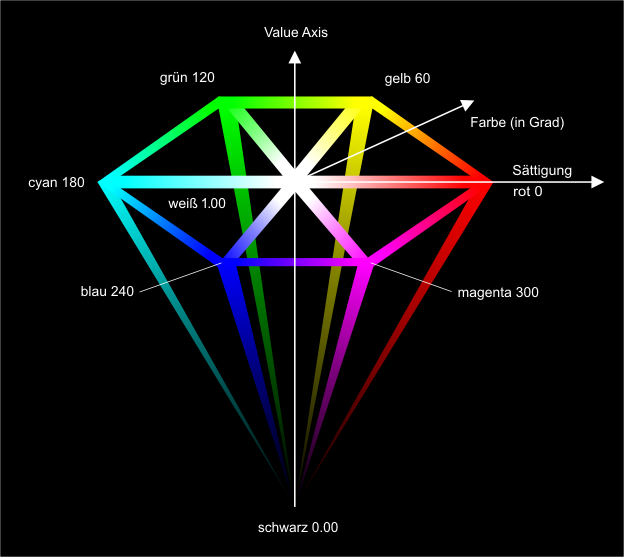
- Bild 4. Den typischen HSV-Hexakegel erhält man, indem man den RGB-Einheitswürfel entlang der Diagonalen von Schwarz nach Weiß projiziert. Es resultiert ein Sechseck, das die Basis der HSV-Pyramide bildet. Jede Farbe wird durch einen Winkel in diesem Sechseck angegeben.
Der Parameter S liegt im Bereich von 0 bis 1 und
repräsentiert das Verhältnis der Reinheit der Farbe zur
maximalen Reinheit, die mit S=1 definiert ist.
Daraus folgt, daß entlang der vertikalen Achse V
die Grauskala liegt, wenn S=0 ist.
Farben besitzen immer einen S-Wert größer 0.
Die Intensität der Farbe schließlich wird über V
bestimmt, der im Bereich von 0 (Schwarz) bis 1 (höchste Helligkeit) liegen kann
Die Arbeit mit dem HSV-Farbmodell
ist denkbar einfach. Durch Angabe eines Winkels wird ein Farbton ausgewählt.
Durch fortlaufendes Reduzieren der Sättigung kann man jeden
Farbton zu Weiß ausbleichen. Ebenso kann jede Einfärbung
durch Reduzierung von V zu Schwarz abgeblendet werden.
Die Umrechnung der RGB-Werte in
HSV-Werte erfolgt
gemäß der bereits besprochenen Projektion des Einheitswürfels auf den Hexakegel.
Die Achse V entspricht der Diagonalen durch den Ursprung (Schwarz)
und Weiß. Der konkrete Wert von V ist gleich dem Maximum der
RGB-Intensitäten. Die Werte
H und S müssen aus der Position
des Punktes im Sechseck berechnet werden, das durch Projektion des kleinsten, den
RGB-Punkt beinhaltenden Würfels erzeugt wird.
Ist S = 0, so ist H nicht definiert,
denn es handelt sich um einen Grauwert und nicht um einen Farbton.
Die Rückrechnung erfolgt durch Umkehren des Algorithmus.
HLS: Blau als Nullpunkt
Ein dem HSV-Farbmodell
ähnliches Modell wurde von Tektronix entwickelt.
Es arbeitet mit den Parametern Hue (Farbe),
L (Lightness,
Helligkeit) und S (Saturation,
Reinheit), woraus der Name HLS-Modell
folgt. Auch hier werden die Farben in Form von Winkel angegeben, jedoch beginnt
HLS mit Blau bei 0 Grad.
Der Parameter S entspricht dem des
HSV-Modells und
liegt ebenfalls im Bereich von 0 bis 1. Für S=0 erhält man
eine Grauskala und für S=1 reine Farben. Obwohl der Parameter
L in etwa dem V des
HSV-Modell entspricht,
gibt es hier jedoch einen entscheidenden Unterschied: HLS
bildet einen Doppelkegel von L=0 (Schwarz) bis L=1 (Weiß),
wobei die maximale Sättigung jedoch bei L=0,5 liegt.
Die Umrechnung der Farben von RGB nach
HLS
erfolgt ähnlich der von RGB nach
HSV.
Mit der Unit FARBE.PAS
(Listing 1)
folgt diesem theoretischen Teil eine Unit,
die alle wichtigen Umrechen-Routinen enthält. Basis aller Konvertierungen ist
immer das RGB-Modell, das in alle anderen
Modelle umgewandelt werden kann. Soll beispielsweise
CMY nach
HLS konvertiert
werden, muß man die CMY-Werte
zunächst in RGB-Werte umrechnen und diese dann in
HLS-Werte konvertieren.
Wer will, kann natürlich Interface-Funktionen für sämtliche Kombinationen schreiben.
Eine größere Verbreitung fanden nämlich nur
RGB und
HLS.
Letzteres wird gerne von Grafikern angewandt.
Das Programm RGBTEST
(Listing 2)
zeigt den Einsatz der Unit FARBE.PAS. Allerdings werden die Eingaben nicht
überprüft. Also bitte korrekte Werte eingeben!
Dietmar Bückart
Listing 1. Die Turbo-Unit FARBE.PAS
UNIT FARBE;
INTERFACE
PROCEDURE RGBtoCMY( r, g, b : REAL;
VAR c, m, y : REAL);
PROCEDURE CMYtoRGB( c, m, y : REAL;
VAR r, g, b : REAL);
PROCEDURE RGBtoYIQ( r, g, b : REAL;
VAR y, i, q : REAL);
PROCEDURE YIQtoRGB( y, i, q : REAL;
VAR r, g, b : REAL);
PROCEDURE RGBtoHSV( r, g, b : REAL;
VAR h, s, v : REAL);
PROCEDURE HSVtoRGB( h, s, v : REAL;
VAR r, g, b : REAL);
PROCEDURE RGBtoHLS( r, g, b : REAL;
VAR h, l, s : REAL);
PROCEDURE HLStoRGB( h, l, s : REAL;
VAR r, g, b : REAL);
IMPLEMENTATION
{ *************************************************************
Bestimmt den kleinsten Wert des RGB-Tipels
Eingabe : r, g, b im Bereich [0.0 .. 1.0]
Rückgabe: kleinster Wert
************************************************************* }
FUNCTION MinRGB(r, g, b : REAL) : REAL;
CONST
RValue : REAL = 1.0;
BEGIN
IF (r < RValue)
THEN RValue := r;
IF (g < RValue)
THEN RValue := g;
IF (b < RValue)
THEN RValue := b;
MinRGB := RValue;
END;
{ *************************************************************
Bestimmt den größten Wert des RGB-Tipels
Eingabe : r, g, b im Bereich [0.0 .. 1.0]
Rückgabe: größter Wert
************************************************************* }
FUNCTION MaxRGB(r, g, b : REAL) : REAL;
CONST
RValue : REAL = 0.0;
BEGIN
IF (r > RValue)
THEN RValue := r;
IF (g > RValue)
THEN RValue := g;
IF (b > RValue)
THEN RValue := b;
MaxRGB := RValue;
END;
{ *************************************************************
Umrechnung RGB --> CMY: PROCEDURE RGBtoCMY
Eingabe: r, g, b im Bereich [0.0 .. 1.0]
Ausgabe: c, m, y im Bereich [0.0 .. 1.0]
************************************************************* }
PROCEDURE RGBtoCMY( r, g, b : REAL;
VAR c, m, y : REAL);
BEGIN
c := 1.0 - r;
m := 1.0 - g;
y := 1.0 - b;
END;
{ *************************************************************
Umrechnung CMY --> RGB: PROCEDURE CMYtoRGB
Eingabe: c, m, y im Bereich [0.0 .. 1.0]
Ausgabe: r, g, b im Bereich [0.0 .. 1.0]
************************************************************* }
PROCEDURE CMYtoRGB( c, m, y : REAL;
VAR r, g, b : REAL);
BEGIN
r := 1.0 - c;
g := 1.0 - m;
b := 1.0 - y;
END;
{ *************************************************************
Umrechnung RGB --> YIQ: PROCEDURE RGBtoYIQ
Eingabe: r, g, b im Bereich [0.0 .. 1.0]
Ausgabe: y, i, q im Bereich [0.0 .. 1.0]
************************************************************* }
PROCEDURE RGBtoYIQ( r, g, b : REAL;
VAR y, i, q : REAL);
BEGIN
y := 0.299 * r + 0.587 * g + 0.114 * b;
i := 0.596 * r - 0.274 * g - 0.322 * b;
q := 0.211 * r - 0.522 * g + 0.311 * b;
END;
{ *************************************************************
Umrechnung YIQ --> RGB: PROCEDURE YIQtoRGB
Eingabe: y, i, q im Bereich [0.0 .. 1.0]
Ausgabe: r, g, b im Bereich [0.0 .. 1.0]
************************************************************* }
PROCEDURE YIQtoRGB( y, i, q : REAL;
VAR r, g, b : REAL);
BEGIN
r := 1.0 * y + 0.956 * i + 0.623 * q;
g := 1.0 * y - 0.272 * i - 0.648 * q;
b := 1.0 * y - 1.105 * i + 1.705 * q;
END;
{ *************************************************************
Umrechnung RGB --> HSV: PROCEDURE RGBtoHSV
Eingabe: r, g, b im Bereich [0.0 .. 1.0]
Ausgabe: h im Bereich [0.0 .. 360.0]
s, v im Bereich [0.0 .. 1.0]
Kommentar: gilt s = 0, dann ist h undefiniert
************************************************************* }
PROCEDURE RGBtoHSV( r, g, b : REAL;
VAR h, s, v : REAL);
VAR
r1, g1, b1, MinValue, HelpValue : REAL;
BEGIN
v := MaxRGB(r, g, b);
MinValue := MinRGB(r, g, b);
HelpValue:= v - MinValue;
IF (v > 0.0)
THEN s := HelpValue / v
ELSE s := 0;
IF (s > 0.0)
THEN BEGIN
r1 := (v - r) / HelpValue;
g1 := (v - g) / HelpValue;
b1 := (v - b) / HelpValue;
IF (v = r)
THEN BEGIN
IF (MinValue = g) { magenta - gelb }
THEN h := 5 + b1
ELSE h := 1 - g1;
END
ELSE IF (v = g)
THEN BEGIN
IF (MinValue = b) { gelb - cyan }
THEN h := 1 + r1
ELSE h := 3 - b1;
END
ELSE BEGIN
IF (MinValue = r) { cyan - magenta }
THEN h := 3 + g1
ELSE h := 5 - r1;
END;
IF (h < 6)
THEN h := h * 60
ELSE h := 0;
END;
END;
{ *************************************************************
Umrechnung HSV --> RGB: PROCEDURE HSVtoRGB
Eingabe: h im Bereich [0.0 .. 360.0]
s, v im Bereich [0.0 .. 1.0]
Ausgabe: r, g, b im Bereich [0.0 .. 1.0]
Kommentar: gilt s = 0, ist h undefiniert
************************************************************* }
PROCEDURE HSVtoRGB( h, s, v : REAL;
VAR r, g, b : REAL);
VAR
iValue : INTEGER;
fValue, s1, s2, s3 : REAL;
PROCEDURE SetRGB(v1, v2, v3 : REAL);
BEGIN
r := v1;
g := v2;
b := v3;
END;
BEGIN
IF (s = 0)
THEN BEGIN
SetRGB(v, v, v); { h ist undefiniert }
EXIT;
END;
h := h / 60;
iValue := TRUNC(h);
fValue := h - iValue;
s1 := v * (1.0 - s);
s2 := v * (1.0 - s * fValue);
s3 := v * (1.0 - s * (1 - fValue));
CASE iValue OF
0 : SetRGB( v, s3, s1);
1 : SetRGB(s2, v, s1);
2 : SetRGB(s1, v, s3);
3 : SetRGB(s1, s2, v);
4 : SetRGB(s3, s1, v);
5 : SetRGB( v, s1, s2);
END;
END;
{ *************************************************************
Umrechnung RGB --> HLS: PROCEDURE RGBtoHLS
Eingabe: r, g, b im Bereich [0.0 .. 1.0]
Ausgabe: h im Bereich [0.0 .. 360.0]
l, s im Bereich [0.0 .. 1.0]
Kommentar: gilt s = 0, dann ist h undefiniert
************************************************************* }
PROCEDURE RGBtoHLS( r, g, b : REAL;
VAR h, l, s : REAL);
VAR
r1, g1, b1, MinValue, MaxValue, HelpValue : REAL;
BEGIN
MaxValue := MaxRGB(r, g, b);
MinValue := MinRGB(r, g, b);
l := (MaxValue + MinValue) / 2;
HelpValue:= MaxValue - MinValue;
IF (HelpValue = 0)
THEN BEGIN
s := 0; { Grauwert }
EXIT;
END;
IF (l > 0.5)
THEN s := HelpValue / (2 - MaxValue - MinValue)
ELSE s := HelpValue / ( MaxValue + MinValue);
r1 := (MaxValue - r) / HelpValue;
g1 := (MaxValue - g) / HelpValue;
b1 := (MaxValue - b) / HelpValue;
IF (MaxValue = r)
THEN BEGIN
IF (MinValue = g) { magenta - gelb }
THEN h := 1 + b1
ELSE h := 3 - g1;
END
ELSE IF (MaxValue = g)
THEN BEGIN
IF (MinValue = b) { gelb - cyan }
THEN h := 3 + r1
ELSE h := 5 - b1;
END
ELSE BEGIN
IF (MinValue = r) { cyan - magenta }
THEN h := 5 + g1
ELSE h := 1 - r1;
END;
IF (h < 6)
THEN h := h * 60
ELSE h := 0;
END;
{ *************************************************************
Umrechnung HLS --> RGB: PROCEDURE HLStoRGB
Eingabe: h im Bereich [0.0 .. 360.0]
l, s im Bereich [0.0 .. 1.0]
Ausgabe: r, g, b im Bereich [0.0 .. 1.0]
Kommentar: gilt s = 0, ist h undefiniert
************************************************************* }
PROCEDURE HLStoRGB( h, l, s : REAL;
VAR r, g, b : REAL);
VAR
s1, s2 : REAL;
FUNCTION Interpol(winkel : INTEGER) : REAL;
VAR
farbe : REAL;
BEGIN
farbe := h + winkel;
IF (farbe > 360)
THEN farbe := farbe - 360;
IF (farbe < 60)
THEN Interpol := s1 + (s2 - s1) * farbe / 60
ELSE IF (farbe < 180)
THEN Interpol := s2
ELSE IF (farbe < 240)
THEN Interpol := s1 + (s2 - s1) * (240 - farbe) / 60
ELSE Interpol := s1;
END;
BEGIN
IF (l > 0.5)
THEN s2 := l + s - l * s
ELSE s2 := l + l * s;
s1 := 2 * l - s2;
IF (s > 0)
THEN BEGIN
r := Interpol(0);
g := Interpol(240);
b := Interpol(120);
END
ELSE BEGIN { h ist undefiniert }
r := l;
g := l;
b := l;
END;
END;
BEGIN
END.
Listing 2. Das Programm RGBTEST.PAS
PROGRAM RGBTEST;
USES CRT, FARBE;
VAR
r, g, b, rVal1, rVal2, rVal3 : REAL;
BEGIN
ClrScr;
Writeln('Konvertieren von RGB-Werten in andere Farbsysteme');
Writeln('Copyright (c) 1991 Dietmar Bückart & mc'^J^M);
Writeln('Geben Sie RGB-Werte im Bereich von [0.0..1.0] ein.');
Write('R: '); Readln(r);
Write('G: '); Readln(g);
Write('B: '); Readln(b);
Writeln;
IF (r < 0.0) OR (r > 1.0) OR
(g < 0.0) OR (g > 1.0) OR
(b < 0.0) OR (b > 1.0)
THEN BEGIN
Writeln('Da war ein ungütiger Wert dabei!');
HALT(1);
END;
Writeln('RGB-Model: R=', r:6:3,
' G=', g:6:3,
' B=', b:6:3);
RGBtoCMY(r, g, b, rVal1, rVal2, rVal3);
Writeln('CMY-Model: C=', rVal1:6:3,
' M=', rVal2:6:3,
' Y=', rVal3:6:3);
RGBtoYIQ(r, g, b, rVal1, rVal2, rVal3);
Writeln('YIQ-Model: Y=', rVal1:6:3,
' I=', rVal2:6:3,
' Q=', rVal3:6:3);
RGBtoHSV(r, g, b, rVal1, rVal2, rVal3);
Writeln('HSV-Model: H=', rVal1:6:1,
' S=', rVal2:6:3,
' V=', rVal3:6:3);
RGBtoHLS(r, g, b, rVal1, rVal2, rVal3);
Writeln('HLS-Model: H=', rVal1:6:1,
' L=', rVal2:6:3,
' S=', rVal3:6:3);
END.aus mc 11/91 – Seite 84-91
