Artikel

Interpolationskurven

Die Interpolation ist ein mathematisches Hilfsmittel, das für jede Art von grafischer Datenpräsentation unerläßlich ist. Im wesentlichen geht es dabei um die Verbindung zweier oder mehrerer Punkte in einem zweidimensionalen Koordinatensystem. Im trivialsten Fall werden zwei Punkte ohne weiteren Rechenaufwand mit einer Geraden verbunden.
Wesentlich komplizierter wird das Ganze, wenn eine Anzahl von Punkten mit einer knickfreien Kurve verbunden werden soll. Was der geübte Zeichner frei Hand zustande bringt, muß der Computer Punkt für Punkt errechnen. Das gebräuchlichste Verfahren zur Bestimmung einer Interpolationskurve beschreibt ein Polynom n-ten Grades. Dabei entspricht die Anzahl der Kurvenstützpunkte n +1

y  =  a (0) + a (1) · x + a (2) · x2 + ... + a (n) · xn

Diese Methode wird jedoch überaus rechenintensiv, wenn die Anzahl der gegebenen Stützpunkte groß ist. Zudem weist die auf diesem Wege errechnete Kurve eine starke "Welligkeit" auf. Wesentlich bessere Ergebnisse liefern die aus der Technik bekannten sogenannten Spline-Funktionen. Mit ihnen gelingen knickfreie Interpolationskurven kleinster Krümmung und geringer Welligkeit. Die Behandlung der Splines erfordert jedoch das Lösen umfangreicher Gleichungssysteme. Zudem wird damit die Interpolation komplizierter als der gesamte Rest eines Programms.
In der Praxis auf Mikrocomputern hat sich ein anderes Verfahren bewährt. Hierbei handelt es sich um modifizierten, kubischen Spline-Funktionen. Die Gesamtkurve wird in mehrere, durch jeweils drei Stützpunkte bestimmte Teilkurven zerlegt. Jedes dieser Kurvenstücke wird so beschrieben:

f1  =  y1 + a1 · (x − x1) + b1 · (x − x1)2 + c1 · (x − x1)3 für x1  ≤  x  ≤  x2
f2  =  y2 + a2 · (x − x2) + b2 · (x − x2)2 + c2 · (x − x2)3 für x2  ≤  x  ≤  x3

Hierbei stehen x1, y1, x2, x3 und y3 für die Koordinaten der drei Kurvenstützpunkte, und es gilt:

h  =  x2 − x1  =  x3 − x2

Die Koeffizienten b1, c1, a2, b2 und c2 werden nach dem folgenden Schema berechnet:

d1  =  y2 − y1
d2  =  y3 − y2
a   =  (2 · d2 − 3 · d1)  /  h2 + a1  /  h
b2  =  2 · a  /  3
b1  =  (3 · d1 − d2)  /  h2 − 2 · a1  /  h + a  /  3
c1 · h  =  (d2 − 2 · d1)  /  h2 + a1  /  h − a  /  3
a2  =  a1 + h · (2 · b1 + 3 + c1 · h)

Der frei wählbare Koeffizient a1 bestimmt die Steigung der Interpolationskurve in ihrem Ausgangspunkt. Nach Berechnung des ersten Kurvenstücks wird die Anschlußkurve nach dem gleichen Schema berechnet. Damit die Kurvenstücke knickfrei aneinander anschließen, wird als Anfangssteigung jeweils die Steigung im Endpunkt der vorangegangenen Teilkurve eingesetzt. Das Programm berechnet die Interpolationskurve recht genau. Der Grafikmodus entspricht der EGA-Norm, für andere Grafikarten sind entsprechende Änderungen erforderlich.

Dr. Georg Seidl

21 Punkte, die mittels einer Spline-Kurve miteinander verbunden sind
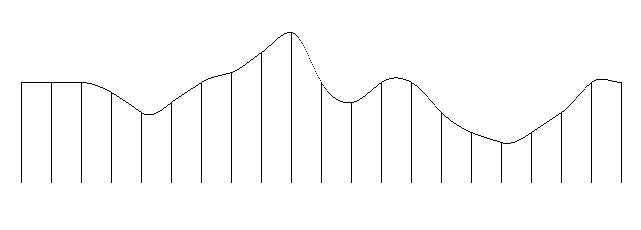
Bild 1: Graph einer interpolierten Kurve
Listing: INTERPOL.BAS
10 REM SPLINE
20 REM G.Seidl , 6/90
30 REM
40 N=20 : H=30
50 DIM Y(N)
60 REM
70 FOR I=0 TO N : READ Y(I) : NEXT
80 REM Meßpunkte zeichnen
90 SCREEN 9 : CLS
100 FOR I=0 TO N
110 X=I*H : Y=Y(I)
120 LINE (X,Y)-(X,200)
130 NEXT
140 GOSUB 170
150 W$=INKEY$ : IF W$="" THEN 150
160 END
170 REM Splineberechnung
180 A1=(Y(1)-Y(0))/H : REM Anfangssteigung
190 FOR I=0 TO N-2 STEP 2
200 Y1=Y(I) : Y2=Y(I+1) : Y3=Y(I+2)
210 GOSUB 330 : REM Spline-Koeffizienten holen
220 FOR X=0 TO H
230 XX=X+I*H
240 YY=Y1+A1*X+B1*X^2+C1*X^3
250 PSET (XX,YY)
260 XX=H+X+I*H
270 YY=Y2+A2*X+B2*X^2+C2*X^3
280 PSET (XX,YY)
290 NEXT
300 A1=A2+2*B2*H+3*C2*H^2
310 NEXT
320 RETURN
330 REM Berechnung der Spline-Koeffizienten
340 D1=Y2-Y1:D2=Y3-Y2
350 A=(2*D2-3*D1)/H^2+A1/H
360 B2=2*A/3
370 C2=(-A/3)/H
380 B1=(3*D1-D2)/H^2-(2*A1/H)+A/3
390 C1=((D2-2*D1)/H^2+A1/H-A/3)/H
400 A2=A1+H*(2*B1+3*H*C1)
410 RETURN
415 REM y-Werte der Kurvenstützpunkte
420 DATA 100,100,100,110,130,120,100,090,070,050,100,120,100,100
430 DATA 130,150,160,150,130,100,100

 

aus CHIP 09/90 – Seite 185