Inhalt

Schriftgröße

•  PDF-Version

Im Anfang
war das Wort

Crashkurs Compilerbau

Ein richtiger Informatiker muß seinen eigenen XY-Compiler gebaut haben oder sein eigenes Betriebssystem. Das ist so, weil die Techniken, die dabei angewandt werden, sehr spannend sind und weil fast alle Probleme dabei auftauchen, die in der Informatik wesentlich sind. Wir können hier nur ein paar Einblicke in die Anfangsgründe geben. Wir zeigen, wie interessant das alles ist und was man wissen muß, um den Artikel über Compiler-Compiler zu verstehen.

Assembler

Jedermann weiß, daß Maschinenbefehle im Computerspeicher binär verschlüsselt sind, genauso die Eingabedaten. Zusammen bilden sie das Maschinenprogramm, das von Hand in Binärform schwer zu lesen, aufzuschreiben und zu manipulieren ist. Aus diesem Grund gibt es Wortsymbole für die Maschinenbefehle und besondere Maschinenprogramme, die Assembler, die sowohl die Wortsymbole als auch Eingabewerte im Klartext erfassen und in Maschinensprache umsetzen. Ein Assembler setzt die Mnemonics, das sind die Wortsymbole, direkt in Maschinenbefehle um. MOV A,B ist ein Beispiel aus der 80XXX-Welt für einen Assemblerbefehl, der den Inhalt von Maschinenregister B in das Maschinenregister A kopiert. Die Aktion, die ein Maschinenbefehl auslöst, das ist seine Semantik, seine Bedeutung. Die Form, die er besitzt, daß nämlich nach MOV zwei durch Komma getrennte Angaben über die gewünschten Speicherstellen (CPU-Register sind auch Speicherzellen) kommen müssen, das ist die Syntax, die grammatikalisch korrekte Form dieses Befehls. Maschinenbauer und Assemblerprogrammierer haben sie so für ihre Maschine vorgegeben. Jede Maschine besitzt ihre eigenen Befehle und Syntax dazu.

MOV A,B
ADD A,C
MOV D,A

ist ein Algorithmus, der erst die Zahl in B nach A schafft, zu ihr die Zahl in C dazuaddiert und dann das Ergebnis nach D bringt. Als Formel: D=B+C.

Compiler und Linguistik

Das kleine Assemblerprogrammstück oben besitzt eine klare Semantik, es addiert zwei (ganze) Maschinenzahlen und liefert das Ergebnis an einer bestimmten Stelle ab. So einfach es aussieht, so wenig übersichtlich ist es, jedesmal für D=B+C solche Assemblerzeilen zu schreiben. Deshalb hat man schon früh begonnen, Assemblerprogramme oder auch Maschinenprogramme zu schreiben, die Formelklartext (und andere Dinge) erfassen und in Maschinensprache umsetzen. Formula Translator, Fortran heißt eines der ersten Programme dieser Art, das bei IBM entwickelt wurde. Heute gibt es viele Programmiersprachen, zum Beispiel Basic (das aus Fortran für Computerneulinge entwickelt wurde), Algol, Pascal, C, Ada, Prolog, ... und immer noch Fortran. So verschieden sie sind, so identisch ist ihre Aufgabe: Man will in ihnen bequem Algorithmen aufschreiben können. Wie man das fehlerfrei machen kann und was man alles über solche Sprachen mitteilen kann, das untersuchen sowohl die Sprachforscher als auch die Informatiker.
Sprachforscher versuchen den Reichtum der natürlichen Sprachen zu erfassen und Erkenntnisse zu gewinnen, weshalb es überhaupt möglich ist, sinnvoll zu sprechen, wie es möglich ist, und was überhaupt alles sagbar ist. In ihrem Bemühen, diesen Fragen nachzugehen, sind die Sprachforscher gewissermaßen von oben herab (weil sie oft fertige Sprachen zu analysieren haben) auf dieselben Erkenntnisse gestoßen, wie sie die Informatiker von unten herauf (weil sie sich geeignete Sprachen konstruieren wollten) erarbeiten mußten. Und es sind dieselben Fragen, die Mathematiker von einem sehr puren, formalen Standpunkt aus immer schon behandelt haben und behandeln werden. Es geht um die rein formale Manipulation von Zeichen- und Symbolketten und was diese dabei an Bedeutung haben könnten.

Mengenlehre

Einer jeden Sprache liegen immer eine Anzahl, eine Menge gewisser Symbole zugrunde, die Grund- oder Terminalsymbole, aus welchen alle syntaktischen Elemente aufgebaut sind. Bei geschriebenen Sprachen ist das oft die Menge der Buchstaben, neudeutsch der ASCII-Zeichensatz, das Alphabet.
Wenn man sinnlos beliebige Symbolketten aus einem Reservoir, einer Menge von Symbolen, zusammenbauen will, so erhält man die Wörter über diesem Alphabet.

abc,
xyzabdef,
unheimlich stark,

das sind Beispiele für unsinnige und sinnvolle Wörter über dem ASCII-Alphabet. Bei Programmiersprachen – das muß man sich klarmachen – sind die Terminalsymbole oft ganze Schlüsselwörter, die zwar aus ASCII-Zeichen zusammengesetzt sind, hier aber selbst als Einheit auftreten. MOV wäre so ein Terminalsymbol aus der Assemblersprache oben und MOV A,B ein sinnvolles Wort.

Grammatik ist Syntax

Aus der Menge der rein kombinatorisch zusammengesetzten Wörter über einer Symbolmenge werden durch die (von Schülern gefürchtete) Grammatik die korrekten Bildungen ausgesondert. Bei den natürlichen Sprachen ist die Grammatik durch die Sprachgewohnheiten vorgegeben – meist nicht eindeutig. Bei Programmiersprachen hat der Compilerbauer die Grammatik vorgegeben, konstruiert. Zum Beispiel sind Namen von Variablen in der Grammatik der meisten Sprachen so konstruiert:
Als erstes muß ein Buchstabenzeichen kommen, dann können bis zu so und soviel weitere Zeichen kommen, Buchstaben oder Ziffern.
Man könnte die grammatikalisch korrekten Wörter über einem Alphabet einfach aufzählen. Dann müßte man beim Arbeiten in einer so definierten Grammatik immer eine Vergleichsliste bei sich führen um die Richtigkeit der gebildeten Wörter kontrollieren zu können. Das mag bei einfachen Grammatiken machbar sein. Falls beliebig lange und beliebig viele Wörter in einer Grammatik vorkommen dürfen, kann eine solche Liste nicht geführt werden.
Weil aber Programme beliebig lang werden dürfen und es auch beliebig viele Programme gibt, haben sich die Informatiker um konstruktive Verfahren bemüht, die es gestatten, die formal korrekten Programme, also Wörter über dem Vorrat der Grundsymbole einer Programmiersprache, systematisch aufzuzählen. Man kann dabei wie folgt vorgehen:

Man nehme die Menge der Grundsymbole G;
man nehme weiter eine Menge V von sogenannten syntaktischen Variablen, die als Platzhalter für grammatikalische Objekte dienen, wobei G und V keine Elemente gemeinsam haben dürfen;
und man nehme einige Hilfszeichen, genannt Metasymbole, die nicht zu den Grundsymbolen und zu V gehören sollen und nur Hilfsmittel sind, die bei der formal präzisen Beschreibung der korrekten Wörter eingesetzt werden.

Zum Beispiel sei G die Menge der ASCII-Zeichen. V bestehe nur aus der Variablen NAME. Aus der Menge der beliebigen Zusammenstellungen von ASCII-Zeichen sollen nur diejenigen als korrekt gebildete Namen gelten, die wie oben für Namen in Programmiersprachen definiert sind. Als einziges Metasymbol nehme man das Zeichen ::=, was als „Ist formal definiert als“ in den folgenden Definitionen gelesen werden kann.

NAME::=a
NAME::=b
...
NAME::=z
NAME::=A
NAME::=B
...
NAME::=Z

ist eine Liste von Regeln, die schon einmal einige korrekte Namen aufzählt. Wobei die einzelnen Zeilen jeweils eine von mehreren Möglichkeiten darstellen, also ein korrekter Name a oder b oder... sein kann. Den Schritt zu beliebig vielen Namen beliebiger Länge kann man durch rekursive Definitionen machen.

NAME::=NAMEa
NAME::=NAMEb
...
NAME::=NAMEz
NAME::=NAMEA
...
NAME::=NAMEZ

was so gelesen werden sollte: Liegt ein bisher korrekt gebildeter NAME vor, dann ist auch das Wort ein korrekter Name, das entsteht, wenn an den korrekten Namen ein weiterer Buchstabe angehängt wird. Diese Liste von rekursiven Definitionen sei jetzt noch um zehn weitere ergänzt, wobei die Ziffern zur Menge der Grundsymbole gehören:

NAME::=NAME0
NAME::=NAME1
...
NAME::=NAME9

Womit erreicht ist, daß korrekte Namen nach dem ersten Buchstaben auch eine Ziffer enthalten dürfen.
Betrachtet man jetzt ein beliebiges Wort über G, zum Beispiel alpha3, dann kann man anhand der vorgegebenen Regeln überprüfen, ob alpha3 ein korrekter Name ist. Ein Weg, dies mechanisch zu tun, lautet:
Man nehme das zu überprüfende Wort, hier also alphaS und teste, ob es als Grundsymbol in einer der Definitionen rechts vorkommt. Falls ja, ist man fertig. Wenn nein, teste man, ob es als zulässige Kombination Name und Buchstabe oder Ziffer rechts vorkommt. Dazu nehme man das letzte Grundsymbol des Wortes und überprüfe anhand der Definitionenliste, ob die Kombination NAME, letztes Grundsymbol in der Liste vorkommt. NAME3 kommt in der Liste vor, ist also ein korrekter Name, wenn alpha ein korrekter Name ist. alpha ist ein korrekter Name, wenn NAMEa ein korrekter Name ist. Das ist der Fall, wenn alph, also NAMEh korrekt ist, das ist der Fall, wenn alp, also NAMEp korrekt ist, wenn also NAME1 korrekt ist und das ist der Fall, wenn a ein Name ist. Das ist durch die Zeile NAME::=a im Definitionen-Schema gesichert. alphaS ist ein korrekter Name. Man hätte hier auch anders vorgehen können und prüfen können, ob das erste Grundsymbol ein zulässiger Beginn eines Namens ist und ob der Name dann gut weitergeht. Zu sehen ist jedenfalls, daß es rein mechanisch entscheidbar ist, ob eine Zeichenkette ein Name ist.

Über eine Sprache reden

Das griechische Wort für „über“ lautet „meta“. Sprachwissenschaftler und Informatiker bezeichnen sprachliche Hilfsmittel zur Behandlung formaler Sprachen als Metasprache. Das Zeichen ::= wurde oben als ein Metasprachenelement, als Metasymbol genutzt. Es hat sich in der Gemeinde der Informatiker die Backus-Naur-Form als Metasprache durchgesetzt, die unter anderem ::= benutzt und dazu zum Beispiel das Zeichen |, das im umgangssprachlichen Sinn „oder“ symbolisiert. Man kann in dieser Form die Definition eines Namens abgekürzt notieren:

Name ::= Buchstabe
Name ::= Name Buchstabe | Name Ziffer
Buchstabe ::= a | b | c | .... X | Y | Z
Ziffer ::= 0 | 1 | 2 | ... 7 | 8 | 9

wenn man noch die Variablen Buchstabe und Ziffer vereinbart.

Zerlegen und Prüfen

Wirft man einem Compiler ein Programm vor (was ja nichts anderes als ein Wort im Sinn unserer Diskussion ist), so beginnt meist als erstes ein Programmteil namens Scanner das Programm zu bearbeiten. Er sucht nach den Grundsymbolen (wozu wie gesagt, neben den Buchstaben auch ganze Wörter der Umgangssprache gehören können) und präsentiert sie dem Compiler in abgekürzter Form als sogenannte Token. Solche Token sind die interne Repräsentation der Grundsymbole. Ein Scanner leistet auch teilweise weitergehende Analysearbeit und sucht nach solchen Unterstrukturen, die wie oben zum Beispiel Namen sind und markiert sie. Danach beginnt ein sogenannter Parser mit der Arbeit. Er überprüft Schritt für Schritt, ob das Programm grammatikalisch korrekt ist. Dazu muß er Grammatiktabellen eingebaut haben. Er kann dann Schritt für Schritt die Token von Beginn an überprüfen und in den Regeltabellen nach Einträgen suchen, die den Beginn des Programmes als möglich anzeigen und zeigen, daß das Programm so weitergehen darf. Der Parser sucht also nach den zugelassenen Konstruktionen im Programm und ob es korrekt zusammengesetzt ist.
Man kann es sich ungefähr so vorstellen: Besitzt die Programmiersprache zum Beispiel die Möglichkeit, Formelklartext mit +, *, (, ) zu verarbeiten, dann könnte sie in einfachen Fällen eine Teilsprache besitzen, die die Grundsymbole

+, *, (, ), ZAHL

und die syntaktischen Symbole

ERGEBNIS, AUSDRUCK, VARIABLE

enthält. In Backus-Naur-Form könnte die Teilgrammatik lauten:

ERGEBNIS ::= AUSDRUCK | ERGEBNIS + AUSDRUCK
AUSDRUCK ::= VARIABLE | AUSDRUCK * VARIABLE
VARIABLE ::= ZAHL | (ERGEBNIS)

wobei jede „Formel“ zu einem Ziel, zum ERGEBNIS führen soll.

Strukturbäume zur Grammatik

Ist ein algebraischer Ausdruck gegeben, zum Beispiel

ZAHL + ( ZAHL *.459 ZAHL )

dann kann man wie oben bei den Namen überprüfen, ob diese Bildung zugelassen ist. Das heißt, ob ein Weg zum ERGEBNIS führt. Das gelingt, wenn man über dem vorgelegten Ausdruck den Codebaum errichtet, der entsteht, wenn man den Ausdruck anhand der Regeln zurückverfolgt (Bild 1).

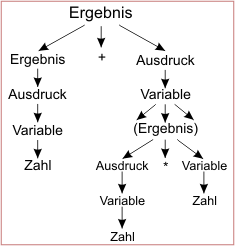
Ein Baum zu einem vorgelegten Ausdruck. Hier wird durch Fortschreiten von den Blättern zur Wurzel bewiesen, daß ein zugelassenes Ergebnis vorliegt.

Die Pfeile geben dabei die Herkunft einer Einheit an, wie sie durch ::= in den Grammatikregeln angegeben ist (aber umgekehrt). Man leitet gewissermaßen durch Fortschreiten im Baum – von den Blättern zur Wurzel – ab, daß man das Endergebnis erreichen kann. Ein syntaktisch inkorrekter Ausdruck würde nicht auf ERGEBNIS führen. Umgekehrt kann man durch systematisches Abwandern aller möglichen Äste von ERGEBNIS aus jede zulässige Formel erzeugen.

Die Codeerzeugung

Hat der Parser zum Beispiel durch Abwandern des zugehörigen Baumes bestimmte Teilkonstruktionen eines Programmes erkannt, so kann er sie einem Codeerzeuger weiterreichen. Der setzt dann in das bisherige Übersetzungsergebnis den zur erkannten Teilkonstruktion zugehörigen Code ein. Das ist ein bißchen leichter gesagt, als getan, denn schon bei einem Assembler muß die Konstruktion MOV A,B mit den sinnvollen Adressen von A und B versehen werden können. Aber es ist bei einer richtig definierten Sprache ohne weiteres ganz mechanisch möglich, die semantischen Aktionen zu einem Programm Schritt für Schritt aus dem Programmtext abzuleiten und in den ausführbaren Code einzufügen. Die Hauptaufgabe eines Compilers ist also die Erkennung von syntaktisch richtigem Programmcode und die Erzeugung des zugehörigen Maschinencodes. Darüber hinaus sollte er natürlich möglichst viele Fehler erkennen und melden, optimieren und, und, und...

Die Metasprache

Der Witz ist, daß man über formale Sprachen in einer formalen Sprache „reden“ kann. Das Metasymbol ::=, das oben zur Formalisierung einer Redeweise diente, kann Grundsymbol einer Sprache sein, mit der man Sprachkonstruktionen beschreiben kann. Oder anders gesagt, man kann die Backus-Naur-Form-Sprache in Backus Naur-Form beschreiben. Das heißt nichts anderes, als daß man einen Compiler bauen kann, der als Semantik in Backus-Naur-Form geschriebene Regeln in einen Parser umsetzt. Ein solcher Compiler ist YACC, den Rolf-Dieter Klein im anschließenden Artikel beschreiben wird. Mit diesem Compiler-Compiler hat er den i860-Assembler entworfen. Das ist eine technologische Leistung, die ihm keiner so schnell nachmacht.

Ulrich Rohde

 

aus mc 04/91 – Seite 174-177

Copyright © 2000 - 2010 by Markus Gans
E-Mail: guru.mail [at] muenster [punkt] de