Artikel
Immer geradeaus
Wenn Sie sich bereits mit der Erzeugung von Grafiken befaßt haben, konnten Sie eine Programmieraufgabe sicher nicht umgehen: das Zeichnen gerader Linien. Ein besonders zügiges Verfahren bietet hier der Bresenham-Algorithmus.
Haben Sie schon selbst an einem Programm zum Zeichnen von Geraden gestrickt? Dabei ist Ihnen vermutlich nicht entgangen, daß die Programmierung eines schnellen und zuverlässigen Verfahrens nicht eben einfach ist. In Ihrer Schulzeit bedienten Sie sich zum Zeichnen von Geraden einer mathematischen Funktion:
f (x) = m · x + bDer Funktionswert »f (x)« (oft auch »y« genannt) stellt eine y-Koordinate dar, die zu einem bekannten x-Wert gehört. Dazu müssen die Parameter »m« und »b« bekannt sein. »m« ist die »Steigung« der Geraden, »b« der »Achsenabschnitt«. Ohne Addition des konstanten Faktors »b« würde jede Gerade durch den Nullpunkt laufen, sofern sie lang genug ist. »b« verschiebt nun den Punkt (0,0) der Geraden, der im Ursprung liegt, auf der y-Achse nach oben oder unten.
Sind die Parameter einmal bekannt, können Sie in einer Schleife einige Werte für »x« in die Funktionsgleichung einsetzen und daraus die y-Werte berechnen. Das Problem besteht darin, die exakte Gleichung zu finden. Im Programmieralltag sieht die Aufgabenstellung für das Zeichnen von Geraden in der Regel so aus: Zwei Punkte sind bekannt, und sollen durch eine Linie verbunden werden. Also beispielsweise die Bildschirmpunkte (100,50) und (200,200).
Die Berechnung des Steigungsparameters »m« für diese Konstellation ist einfach. Sie ergibt sich aus der Formel in Bild 1.
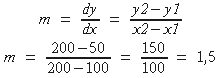
- Bild 1. So berechnen Sie die Steigung einer Geraden
Dabei stehen die beiden Paare (x1,y1) und (x2,y2) für die Koordinaten von zwei beliebigen Punkten auf der Geraden. Im Beispiel mit den Punkten (100,50) und (200,200) ergibt sich eine Steigung von 1,5 (Bild 1). Den Wert für den Achsenabschnitt »b« erhalten Sie durch Auflösen der Funktionsgleichung nach »b«:
b = f (x) − m · xFür »m« setzen Sie den soeben errechneten Wert ein, »f (x)« ersetzen Sie durch eine der beiden y-Koordinaten und »x« durch den Wert der dazugehörigen x-Koordinate. Das Beispiel ergibt:
b = 200 − 200 · 1,5 = −100im einen Fall, und
b = 50 − 100 · 1,5 = −100Sobald »b« und »m« bekannt sind, läßt sich der Algorithmus recht einfach in ein Programm umsetzen. »line.pas« zeigt das Zeichnen der Linie zwischen (100,50) und (200,200) in einem Pascal-Programm (Listing 1).
Eine kleine Überraschung entsteht dadurch, daß bei den bisherigen Betrachtungen der Ursprung links unten im Koordinatensystem lag. Turbo Pascal legt den Ursprung aber in die linke obere Ecke. Die Linie auf dem Bildschirm hat deshalb die Steigung −1,5.
Umständliche Fließkommaberechnungen bremsen einen einfachen Algorithmus
Testen Sie das Programm mit unterschiedlichen Werten, werden Sie bemerken, daß es mit manchen Steigungen nicht korrekt arbeitet. Zwar ließe sich dieses Problem beheben, wesentlicher ist jedoch eine andere Schwäche des Verfahrens: Es arbeitet sehr langsam.
Grundlegendes Problem des Algorithmus ist, daß er ohne Fließkomma-Arithmetik nicht auskommt. Diese Rechnungen sind zeitaufwendig und bremsen die Methode entsprechend. Schneller zeichnen Sie Linien mit dem Bresenham-Algorithmus, einem Verfahren, das der Informatiker J. E. Bresenham entwickelte und 1965 erstmals veröffentlichte. Der Bresenham-Algorithmus beruht im wesentlichen auf zwei Voraussetzungen: Erstens muß ein Algorithmus zum Zeichnen von Linien lediglich in der Lage sein, Geraden mit einer Steigung zwischen null und eins zu zeichnen. Bild 2 zeigt, in welchem Bereich sich solche Geraden bewegen dürfen. Zweitens nimmt Bresenham an, daß für solche Geraden generell nur zwei Punkte als nächste Bildpunkte der Geraden in Betracht kommen, wenn ein Punkt bereits bekannt ist.
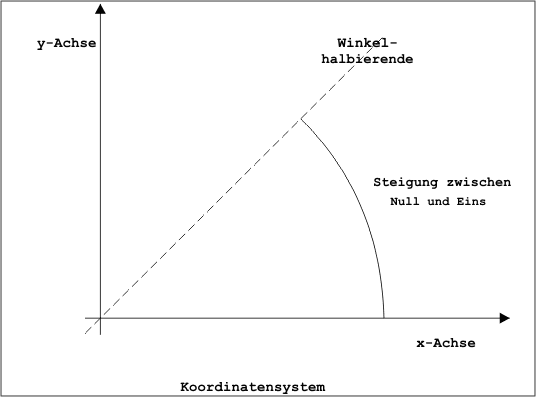
- Bild 2. Geraden mit einer Steigung von null bis eins
Zur ersten These: Was soll mit Geraden geschehen, die steiler verlaufen, also nicht in den Bereich null bis eins passen? Sehen Sie sich Bild 3 an. Die Abbildung zeigt links eine Gerade, deren Steigung über eins hinausgeht. Spiegeln Sie die Gerade an der Winkelhalbierenden, resultiert daraus eine Gerade mit einer Steigung zwischen null und eins. Die Spiegelung an der Winkelhalbierenden aber ist ein einfaches Verfahren: Es reicht aus, die x- und y-Koordinaten eines jeden Punktes auszutauschen.
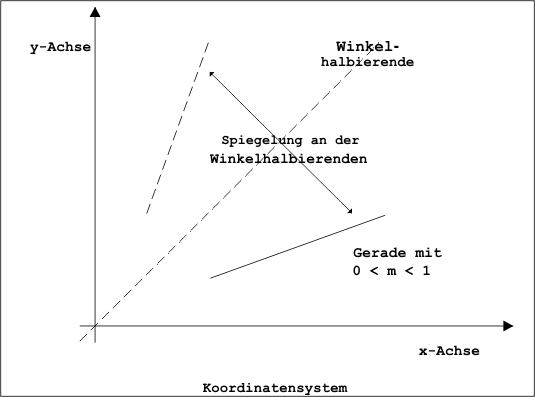
- Bild 3. Geraden mit größerer Steigung lassen sich spiegeln
Zu steile Geraden spiegeln Sie an der Winkelhalbierenden
Wenn der Bresenham-Algorithmus also feststellt, daß die Steigung einer Geraden nicht im Bereich null bis eins liegt, spiegelt er die Ausgangskoordinaten. Es ergibt sich eine Steigung im Bereich null bis eins. Die Berechnung der Punkte führt er mit dieser Geraden durch. Vor dem Zeichnen spiegelt er die berechneten Punkte wieder zurück. Das Verfahren ist einfach und schnell zu realisieren, ohne große Umrechnungsroutinen.
Lassen sich alle Steigungen zeichnen, bleibt die Frage nach negativen Steigungen, also »fallenden« Geraden. Hier hilft der Bresenham-Algorithmus mit dem gleichen Trick weiter. Fallende Geraden werden zu steigenden, wenn Sie sie an der x-Achse spiegeln. Das wiederum erreichen Sie durch ein Umdrehen des Vorzeichens aller y-Koordinaten. Sie sehen, Bresenham hat das Problem des Linienzeichnens wirklich auf Geraden mit einer Steigung von null bis eins beschränkt.
Und hier setzt seine zweite Voraussetzung an. Er behauptet, bei diesen Geraden sei die aufwendige Berechnung der y-Koordinaten über die Steigung unnötig, weil grundsätzlich nur zwei Punkte als Kandidaten für den nächsten Geradenpunkt in Betracht kommen, wenn ein Punkt bereits bekannt ist.
Bild 4 zeigt das Prinzip: Im oberen Bereich ist der Verlauf einer Linie auf dem Bildschirm zu sehen. Der theoretische Verlauf der exakten mathematischen Geraden wird durch die Auswahl der geeigneten Bildpunkte bestmöglich nachgebildet. Im unteren Bereich der Abbildung sehen Sie eine Detailansicht der Geraden. Die beiden Punkte links sollen bereits gezeichnet sein.
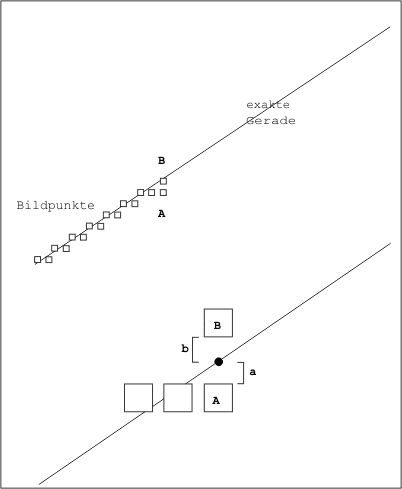
- Bild 4. Nur Punkt A oder B kommt für die Gerade in Frage
Für den dritten Punkt kommen nur zwei Kandidaten in Frage. In der Abbildung sind sie als »A« und »B« gekennzeichnet. Welcher Punkt von beiden auszuwählen ist, ergibt sich daraus, welcher näher an der mathematischen Geraden liegt. Daher gilt, die beiden Abstände »a« und »b« in der Zeichnung zu vergleichen. Wenn »a« kleiner ist, erhält Punkt »A« den Zuschlag, andernfalls Punkt »B«.
Bresenham reduziert das Problem auf die Entscheidung zwischen zwei Punkten
Auf der Basis der Geradensteigungsgleichung löst Bresenham diese Frage mathematisch auf. Die Umformung des Terms ist zwar nicht wirklich kompliziert, setzt aber mathematische Standfestigkeit voraus.
Ergebnis des Bresenham-Algorithmus: Die Differenz der beiden Punkte »A« und »B« beträgt entweder »2 · dy« (falls zuvor Punkt »B« gesetzt wurde) oder »2 · dy − dx« (falls zuletzt Punkt »A« gesetzt wurde). Die Parameter »dx« und »dy« stehen dabei für die Differenz zweier beliebiger x- und y-Koordinaten von Punkten auf der Geraden.
Bahnbrechend an dieser Erkenntnis ist die Tatsache, daß es sich bei beiden Ausdrücken um Konstanten handelt, die Sie einmal zu Beginn des Programms ermitteln können und die sich im Verlauf des Zeichnens nicht mehr verändern. Außerdem handelt es sich um ganzzahlige Werte. Dadurch ist der Einsatz von Fließkomma-Arithmetik überflüssig.
Zu Beginn des Zeichenvorgangs müssen Sie sich nur entscheiden, ob Punkt »A« oder »B« zu setzen ist. Danach können Sie neue Punkte schlicht und einfach durch Addition ganzzahliger Konstanten bestimmen.
Die erste Entscheidung fällt dabei auch nicht schwer. Der erste Punkt der Geraden befindet sich definitionsgemäß an den Koordinaten (0,0), die Sie dann später in das Koordinatensystem auf dem Bildschirm transponieren. Den zweiten Punkt legen Sie einfach bei (1,0) fest.
In »bline.pas« sehen Sie, wie das Verfahren in ein Pascal-Programm umgesetzt aussieht (Listing 2). Als Beispiel zeichnet die Routine wieder eine Gerade von den Koordinaten (100,50) zu (200,200). Wirklich zügig läuft jedoch auch dieses Programm noch nicht. Der Grund dafür liegt in der Programmiersprache. Effektiv arbeitet der Algorithmus nur, wenn Sie das Programm gleich in Assembler formulieren. Das ist bei »fastline.asm« geschehen (Listing 3).
Das Programm setzt alle Tricks effektiver Programmierung ein, beispielsweise selbstmodifizierenden Code und andere Optimierungsstrategien. Da diese Techniken ein Programm in der Regel schneller, aber unübersichtlicher machen, ist das Listing ausführlich kommentiert.
Alle Listings rufen zum Zeichnen der Punkte auf dem Bildschirm die BIOS-Funktion 0Chex von Interrupt 10hex auf. Die Beispielprogramme setzen aus Kompatibilitätsgründen den Videomodus 04hex ein, der ab der CGA-Karte verfügbar ist.
(Martin Althaus/wn)
{Programm: line.pas
Funktion: Linie ziehen mit einfachem Algorithmus
Sprache : Turbo Pascal
Autor : Martin Althaus
(C)1991 DMV Widuch GmbH & Co. KG}
program linie;
uses Dos,Crt;
var cpu: Registers;
merke: Byte;
function altermodus: Byte;
{ Ermittelt den aktuellen Videomodus }
begin
cpu.ah:=$0F;
Intr($10,cpu);
altermodus:=cpu.al;
end;
procedure vmode (modus: Byte);
{Setzt einen Videomodus über die BIOS-
Funktion 00h von Interrupt 10h. übergeben
wird der Prozedur ein Byte für den Video-
modus, der gewählt werden soll. }
begin
cpu.ah:=0; {BIOS-Funktion 00h}
cpu.al:=modus; {gewünschter Modus}
Intr($10,cpu) {Video-BIOS aufrufen}
end;
procedure setzepunkt(x,y: Word; farbe: Byte);
{Setzt einen Punkt an der Koordinate x,y
im aktuellen Video-Modus. Dazu wird
Funktion 00h des Interrupts 10h auf-
gerufen. }
begin
cpu.cx:=x; {X-Koordinate übertragen}
cpu.dx:=y; {Y-Koordinate übertragen}
cpu.al:=farbe; {Farbe übertragen}
cpu.ah:=$0C; {Funktion 0Ch wählen}
Intr($10,cpu); {Interrupt auslösen}
end;
procedure tausche(var a,b: Word);
{ Tauscht den Inhalt von zwei Word-Variablen aus }
var dummy: Word; {Hilfsvariable}
begin
dummy:=a; {Inhalt von A merken}
a:=b; {A wird zu B}
b:=dummy; {B wird zu A}
end;
procedure Line(x1,y1,x2,y2: Word; farbe: Byte);
{Zieht eine Linie zwischen den Punkten
(X1,Y1) und (X2,Y2). Dazu werden die
Punkte gemäß des Geradensteigungs-Algo-
rithmus inkrementell berechnet.}
var y: Integer;
m,b: real;
begin
if x2<x1 then
begin
tausche(x1,x2);
tausche(y1,y2);
end;
if x2<>x1 then
begin
m:=(y2-y1)/(x2-x1);
b:=y1-m*x1;
for x1:=x1 to x2 do
begin
y:=Trunc(m*x1+b);
setzepunkt(x1,y,farbe);
end;
end
else
begin
if y2<y1 then tausche(y1,y2);
for y1:=y1 to y2 do setzepunkt(x1,y1,farbe);
end;
end;
{ Hauptprogramm: Setzt Videomodus und zieht eine Linie }
var dummy: Char;
zaehler: Integer;
y: Word;
begin
merke:=altermodus;
WriteLn('Setze Videomodus 4hex (CGA)');
WriteLn('und ziehe eine Gerade. ');
Write('Bitte mit <Return> bestätigen ');
repeat
until ReadKey=Chr(13);
vmode($4);
for zaehler:=0 to 199 do
Line(0,0,319,zaehler,zaehler AND 3);
repeat
until ReadKey=Chr(13);
vmode(merke);
end.
{Programm: bline.pas
Funktion: Linie ziehen mit Bresenham-Algorithmus
Sprache : Turbo Pascal
Autor : Martin Althaus
(c)1991 DMV Widuch GmbH & Co. KG}
program bline;
uses Dos,Crt;
var cpu: Registers;
merke: Byte;
function altermodus: Byte;
{ Ermittelt den aktuellen Videomodus }
begin
cpu.ah:=$0F;
Intr($10,cpu);
altermodus:=cpu.al;
end;
procedure vmode(modus: Byte);
{Setzt einen Videomodus über die BIOS-
Funktion 00h von Interrupt 10h. übergeben
wird der Prozedur ein Byte für den Video-
modus, der gewählt werden soll. }
begin
cpu.ah:=0; {BIOS-Funktion 00h}
cpu.al:=modus; {gewünschter Modus}
Intr($10,cpu) {Video-BIOS aufrufen}
end;
procedure setzepunkt(x,y: Word; farbe: Byte);
{ Setzt einen Punkt an der Koordinate X,Y im
aktuellen Video-Modus. Dazu wird Funktion
00hex des Interrupts 10hex aufgerufen. }
begin
cpu.cx:=x; {X-Koordinate übertragen}
cpu.dx:=y; {Y-Koordinate übertragen}
cpu.al:=farbe; {Farbe übertragen}
cpu.ah:=$0C; {Funktion 0Chex wählen}
Intr($10,cpu); {Interrupt auslösen}
end;
procedure tausche(var a,b: Word);
{ Tauscht den Inhalt von zwei Word-Variablen aus }
var dummy: Word; {Hilfsvariable}
begin
dummy:=a; {Inhalt von A merken}
a:=b; {A wird zu B}
b:=dummy; {B wird zu A}
end;
procedure Line(x1,y1,x2,y2: Word; farbe: Byte);
{Zieht eine Linie zwischen den Punkten
(X1,Y1) und (X2,Y2). Dazu werden die
Punkte gemäß des Bresenham-Algorithmus
inkrementell berechnet. Sie werden dann
mit der Farbe FARBE versehen. }
var dx,dy,dab: Integer;
incA,incB,incY: Integer;
x,y: Integer; {Die Endkoordinaten}
begin
if x2<x1 then {Müßen Koordianten ge-}
begin {tauscht werden?}
tausche(x1,x2); {Ja, tausche sie}
tausche(y1,y2); {beide aus}
end;
if (y1<y2) {Steigung positiv?}
then {ja, also muß Y in}
incY:=1 {der Schleife erhöht werden}
else {Steigung negativ, also}
incY:=-1; {muß Y abgezogen werden}
dx:=x2-x1; {Berechne die Konstanten:}
dy:=y2-y1; {DX, DY, den Anfangswert für}
dab:=(dy SHL 1)-dx; {Differenz (b-a)}
incA:=(dy-dx) SHL 1; {die alternativen}
incB:=dy SHL 1; {Werte für X-Inkrement}
x:=x1; {der erste Punkt ist der}
y:=y1; {Anfangspunkt}
setzepunkt(x,y,farbe); {setze ihn}
for x:=x1+1 to x2 do {setze in Schleife}
begin
{die Linie}
if dab<0 then {Zuletzt A gesetzt,}
begin
{also ändere das Inkrement}
dab:=dab+incB; {und}
setzepunkt(x,y,farbe);
{setzt den neuen Punkt}
end {Es wurde zuletzt B gesetzt,}
else {also ändere das Inkrement}
begin
{und bereite neue Koordinaten}
y:=y+incY; {zum Setzen vor}
dab:=dab+incA;
setzepunkt(x,y,farbe);
end;
end; {Ende der Schleife}
end;
{ Hauptprogramm: Setzt Videomodus und zieht eine Linie }
var
dummy: Char;
zaehler: Word;
y: Word;
begin
merke:=altermodus;
WriteLn('Setze Videomodus 4hex (CGA)');
WriteLn('und ziehe eine Gerade. ');
Write('Bitte mit <Return> bestätigen ');
repeat
until ReadKey=Chr(13);
vmode(4);
for zaehler:=0 to 199 do
Line(0,0,319,zaehler,zaehler AND 3);
repeat
until ReadKey=Chr(13);
vmode(merke);
end.
;Programm: fastline.asm
;Funktion: Linienzeichnen mit Bresenham-Algorithmus
;Sprache : MASM ab 4.0
;Autor : Martin Althaus
;(c) 1991 DMV Widuch GmbH & Co KG
stack512 segment para stack 'stack'
dw 100h dup (?)
stack512 ends
;
data segment para 'data'
farbe db 0
data ends
;
code segment para 'code'
assume cs:code, ds:data
assume ss:stack512
fastline:
mov ax,data
mov ds,ax
mov ah,0fh ;Videomodus
int 10h ;auslesen
push ax ;und speichern
mov ax,4 ;Modus 04hex
int 10h ;setzen
;
;In einer Schleife einige Geraden zeichnen
;
mov cx,198 ;99 Linien
linie: mov ax,0 ;X1=0
mov bx,198
sub bx,cx ;Y1=0,1,2,3..
mov di,319
mov es,di ;X2=319
mov di,cx ;Y2=198,197...
push cx ;Schleife merken
mov ch,cl ;Farbe setzen
call line ;Linie zeichnen
pop cx ;Schleife zurück
loop linie ;und schließen
;
;Taste abwarten und alten Videomode setzen
;
xor ax,ax
int 16h
pop ax ;hole alten Mode
xor ah,ah ;über Funktion 0
int 10h ;setzen
;
;Programm über DOS beenden
;
mov ax,4c00h ;über 4Chex
int 21h ;beenden
;
;Zeichnet eine Linie zwischen Pl und P2
;nach dem Bresenham-Algorithmus
;
;Parameter: AX=X1 ES=X2
; BX=Y1 DI=Y2
; CH=Farbe
;
line proc near
push bp ;BP retten
;
;Koordinaten speichern
;
push ax ;X1 und
push bx ;Y1 retten
mov farbe,ch ;Farbe speichern
mov bx,4340h ;Code für INC BX
;und INC AX
;
;Ist DELTAX positiv?
;
mov cx,es ;X2 laden und
sub cx,ax ;DELTAX=X2-X1
jge deltax_p0 ;X2>X1?
;
;Nein, also |DELTAX| bilden
;
mov bl,48h ;Code für DEC AX
neg cx ;u. DELTAX umdr.
deltax_p0:
mov dx,di ;Y2 laden
pop si ;Y1 laden
push si ;und retten
;
;|DELTAY| bilden und Laufvariable bestimmen
;
sub dx,si ;DELTAY=Y2-Y1
jge deltay_p0 ;Y2>Y1?
mov bh,4bh ;Code für DEC BX
neg dx ;u. DELTAY umdr.
deltay_p0:
mov si,offset cs:dabgross0
;Ink/Dek im Code
mov word ptr cs:[si],bx
;abspeichern
cmp cx,dx ;DELTAX>DELTAY?
jge deltax_gr0 ;ja, verzweige
mov bl,90h ;Y ist Laufvar.
;für X NOP
xchg cx,dx ;DELTAX und
;DELTAY tauschen
jmp achse0 ;und weiterm.
deltax_gr0:
mov bh,90h ;X ist Laufvariable
;für Y NOP eintragen
;
;Konstanten berechnen
;
achse0: mov si,offset cs:dabklein0
;Ink. für Laufvariable
mov word ptr cs:[si],bx
;im Code ablegen
shl dx,1 ;INCB bestimmen
mov bp,dx ;nach BP übertragen
sub dx,cx ;DAB bestimmen
mov di,dx ;und nach BX
sub dx,cx ;INCA nach DX
pop bx ;Y1 und
pop ax ;X1 laden
;
;Schleife zum Setzen der Punkte der Linie
;
schleife0:
push di ;alle Register, die
push ax ;verändert werden,
push dx ;auf den Stapel
push bx ;retten
push cx
push si
push es
mov cx, ax ;Punkt wählen
mov dx, bx
mov al,farbe;Farbe laden
mov ah,0ch ;Funktion wählen
int 10h ;und Punkt setzen
pop es
pop si
pop cx
pop bx ;alle Register
pop dx ;vom Stapel holen
pop ax
pop di
cmp di,0 ;DAB>0?
jge dabgross0 ;ja, verzweige
;
;DAB ist kleiner oder gleich null
;
dabklein0:
inc ax ;hier wird der
inc bx ;Code modifiz.
add di,bp ;DAB=DAB+INCB
loop schleife0 ;Schleife schl.
jmp end_line0 ;und weiter
;
;DAB ist größer null
;
dabgross0:
inc ax ;hier wird der
inc bx ;Code modifiz.
add di,dx ;Schleife schl.
loop schleife0 ;und weiter
end_line0:
pop bp ;alten Zustand
ret ;Programm enden
line endp
code ends
end fastlinedes Bresenham-Algorithmus
aus DOS International 02/92 – Seite 180-184
